数字集成电路(2)MOS晶体管
本文最后更新于:2022年10月19日 下午
本人《数字集成电路设计》课程笔记,老师为王仁平。
本文主要讲述MOS晶体管动态特性(寄生电容)和手工计算延时的方法。
第三章 MOS晶体管
1. 数字电路的晶体管——最直观
执行开关功能
非常小的寄生电容
非常高的集成度
相对简单的制造工艺
符号:
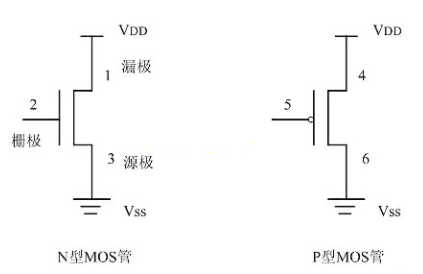
2. MOS静态特性——稳定性(CMOS模电基础)
1. 阈值电压$V_T$
- 考虑体效应对于阈值电压的影响——偏执效应系数 $\gamma$
- 阈值电压与材料常数(氧化层厚度、费米电势、注入离子剂量等)有关
2.三个工作区:
截止—(亚阈值导电)—线性—饱和—(击穿)
3. 沟长调制效应
- 沟长调制系数 $\lambda$: $\lambda$反比于沟长$L$,即沟道长度越短,沟长调制效应越显著。
- 沟长调制效应会使得漏电流$I_D$增大
4. 速度饱和:
短沟道的饱和区范围更大,故常常工作在饱和区。
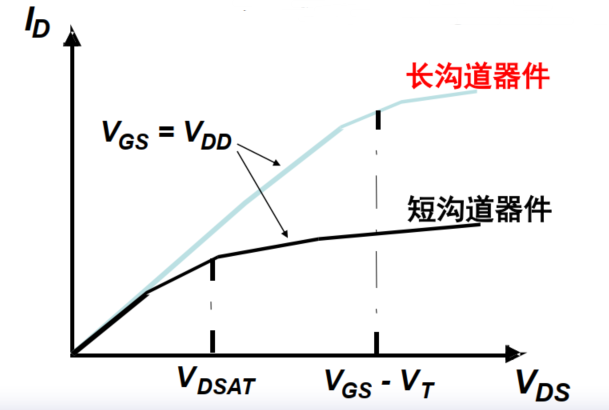
此时,不再用$V_{OV}>V_{GS}-V_{T}$来表征是否进入饱和区,而是使用$V_{DSAT}$表征是否进入饱和区。
5. 漏电流$I_D$和$V_{GS}$
长沟道,呈现平方关系
短沟道,不那么显著
3. 数字电路手工分析模型——开关+$R_{eq}$
常用开关模型——晶体管=开关+无穷大断开电阻$R_{on}$ or 有限导通电阻$R_{on}$
【计算等效导通电阻$R_{eq}$】:2种方法
在实际情况中,导通电阻$R_{on}$是随工作点而时变的。而我们想要用一个等效的、恒定阻值的电阻$R_{eq}$来表征$R_{on}$。
计算所关心的区域上面的平均电阻值:
【常用】使用瞬态过程中,起点和重点两个电阻的平均值
4. 【重点】MOS管的动态特性——性能($t_p$)
1. 电容的分类
MOS管的动态响应取决于:
本征电容:
- 基本的MOS结构:结构电容
- 沟道电荷:沟道电容
- 漏源反向偏置的PN结耗尽电容:结电容
注意:除了结构电容外,其他两个电容是非线性、随电压变化的
寄生电容(连线和负载引起)
2. 略解本征电容
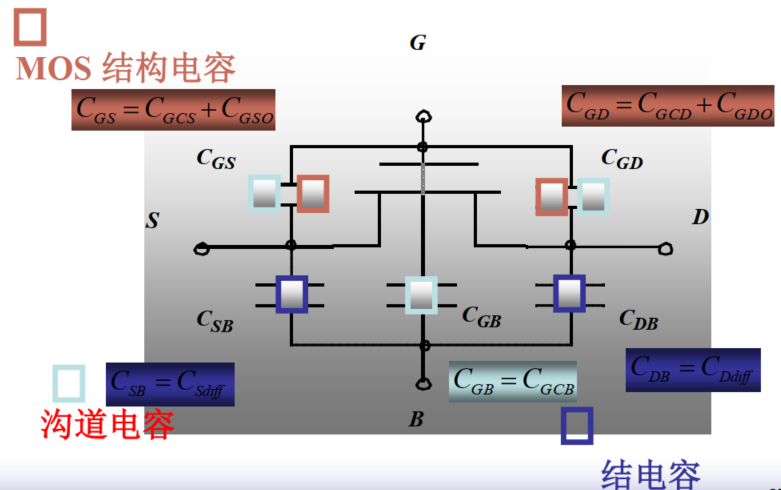
简单归类:
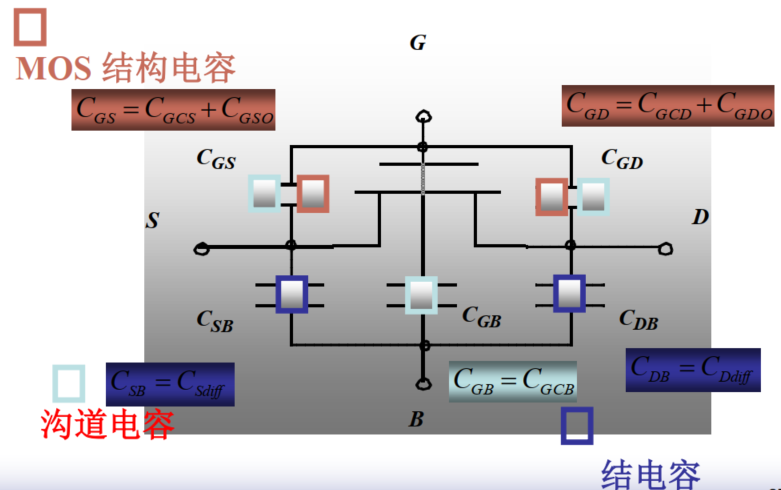
小贴士:$\color{red}{红色框框}$:结构电容;$\color{gray}{灰色框框}$:沟道电容;$\color{blue}{蓝色框框}$:结电容
1. 两个覆盖(结构)电容:
覆盖电容是由于源漏横向扩散到栅氧下形成的寄生电容,故而有两个——栅源之间($C_{GSO}$)和栅漏之间($C_{GDO}$)
由于这个电容是由于扩散形成的,只要器件做成之后就电容大小就确定,于是结构电容是三类电容中唯一可以确定确切大小的
小贴士:由$C_{ox}={\varepsilon}_{ox}/t_{ox}$,于是我们希望$C_{ox}$尽可能的大,因为根据$I_D-V_{DS}$的公式,$I_D\varpropto C_{ox}$
2. 三个沟道电容:
沟道电容,即栅到沟道之间的电容,称为$C_{GC}$,即 (Gate Channel)。其中,
即,栅至体、栅至源、栅至漏电容。
由于和沟道有关,又因为沟道形成和工作点有关,于是三个工作点下,$C_{GC}$不同。
| 工作区域 | $C_{GCB}$ | $C_{GCS}$ | $C_{GCD}$ | 总沟道电容:$C_{GC}$ |
|---|---|---|---|---|
| 截止区 | $C_{ox}WL$ | 0 | 0 | $C_{ox}WL$ |
| 线性区 | 0 | $C_{ox}WL/2$ | $C_{ox}WL/2$ | $C_{ox}WL$ |
| 饱和区 | 0 | $(2/3)C_{ox}WL$ | 0 | $(2/3)C_{ox}WL$ |
以下进行粗略解释:
截止区,沟道未形成,沟道电容只存在于栅体之间。
线性区,反型层形成,且栅源和栅漏反型层对称,故$C_{GCB}$=$C_{GCD}$;
反型层的形成,屏蔽了栅体,故电容为0。
饱和区,沟道被夹断,电容只存在于栅源,另外两部分为0。
关于表格中数值的由来:前面提到,沟道电容是随着电压时变、非线性的,无法用一个值直接表征。表格中的值,是利用逐段线性得到的一个模型值,故而表头称之为“平均分布情况”。
3. 两个(PN)结(耗尽层)电容:
PN结电容是由于源-体和漏-体之间反向偏置造成的。
由于工艺上面,我们是在体上“挖一个坑“放漏和源,故而他们之间存在着”立体“的关系。
故而需要关注”四周立体接触“,如图所示,
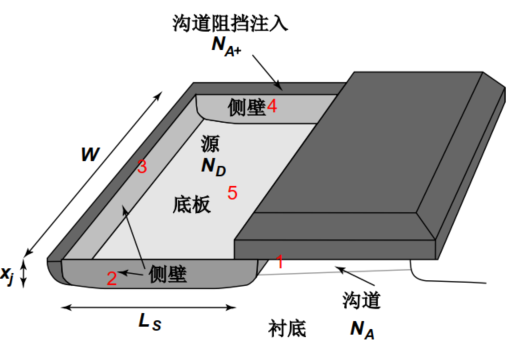
下面对公式稍作解释:
结电容=底板PN结电容+侧壁PN结电容,分为两部分是因为底板体电极是$P$掺杂,而侧壁体电极是$P^+$掺杂;而源/漏都是$N^+$掺杂。
结电容是非线性的,反向偏置增强,结电容减小(反比)
这里不考虑”1“边(源/漏-沟道)侧的侧边电容,故而只有1个$W$,而不是2个$W$。
$C_j$是单位面积底板结电容;$C_{jsw}$是单位周长侧壁结电容,$C_{jsw}=C^{’}_{jsw}x_j$。
由于侧壁的体电极掺杂浓度更大,故而$C^{’}_{jsw}>C_j$
3. 我们关注的【本征电容】有哪些
我们研究电容是为了利用$\tau=RC$计算$t_P$的值,故而我们在意的是输入和输出通路上的电容。
1. 输入电容——栅极电容
对于输入,一般采用栅极输入,即$C_{in}=C_G$
经过上面的推导,可以知道
即
即:栅电容=2个覆盖电容+3个沟道电容
| 工作区 | $C_{O}$:覆盖电容(固定的值) | $C_{GC}$:沟道电容 | $C_G$ |
|---|---|---|---|
| 截止区 | $2C_oW$ | $C_{ox}WL$ | $2C_oW+C_{ox}WL$ |
| 线性区 | $2C_oW$ | $C_{ox}WL$ | $2C_oW+C_{ox}WL$ |
| 饱和区 | $2C_oW$ | $(2/3)C_{ox}WL$ | $2C_oW+(2/3)C_{ox}WL$ |
2.输出电容——漏极电容
对于输出,一般采用漏极输出,即$C_{out}=C_D$
经过上面的推导,可以知道
又因在数集中,一般管子只工作在饱和区和截止区,而这两个区域的$C_{GCD}=0$
即有
即:漏电容=1个覆盖电容+1个PN结电容
4. 寄生电阻
源漏区的串联电阻。
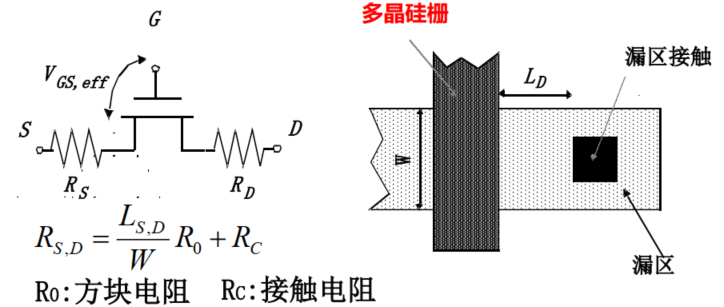
危害:
- 当晶体管尺寸进一步缩小,会使结变浅、接触孔变小。使得这个影响更加显著。
- 当给定一个电压,由于分压作用,会使得漏极电流变小。
改善:
- 源漏极铺一层低电阻材料(如钨或者钛)
5. MOS器件模型
略
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!