本人《数字集成电路设计》课程笔记，老师为王仁平。

本文主要讲述如何根据延时和功耗设计反相器（INV）。

第五章反相器

1. 设计指标

明确：反相器是数字电路设计的核心。

成本：

主要是指标就是面积。在数集中，最小尺寸是$L=2\lambda$，于是【$W$】就成了设计的要点。

$Eg：$

以反相器（$INV$）为例，不同的$W$的INV应用于不同的场合。如：“CLKINV”和”INVD”。CLKINV应用于时间通路上，对延迟要求较高，希望可以做到$t_p≈t_{pLH}≈t_{pHL}$，且尽可能小（或者达到指标）。而对于INVD，并不要求$t_p≈t_{pLH}≈t_{pHL}$，仅需要$t_p=\frac{t_{pLH}+t_{pHL}}{2}$的数值满足要求即可，即如果$t_{pLH}、t_{pHL}$其中一个较小，一个较大，但是平均值满足要求也是可以的。
完整性和稳定性：

主要考虑静态特性

在INV等门电路的设计中，常采用互补CMOS的结构。互补CMOS结构可以让输出的电压上拉到$VDD$或者下拉到$GND$，提高稳定性。
性能：

主要考虑动态特性

也就是【$t_p$】数值大小。
功耗：

使用”关断“等技术

2. INV综述

1. INV的数集模型

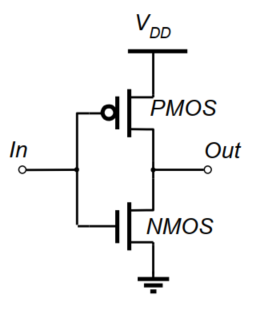
由组成的图可以知道，INV是由两个CMOS管串联组成的。而CMOS的数集模型是理想开关+有限导通电阻or无限关断电阻，故INV的数集模型如下：

INV的开关模型

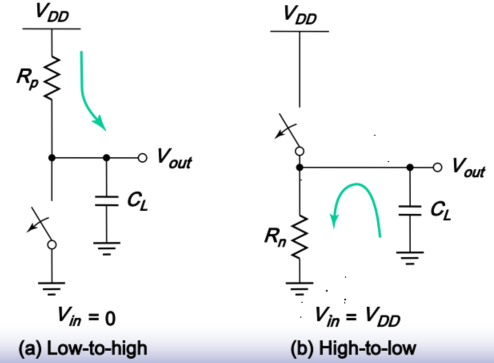
即两个电阻开关并联。

图中的$C_L$表示晶体管的漏极电容、连线电容、扇出门的输入电容

2. INV的特性综述

1. 动态特性：

主要由$C_L$决定，$C_L$表示晶体管的漏极电容、连线电容、扇出门的输入电容

2. 静态特性：

噪声容量大：

电压摆幅=电源电压。因为是CMOS互补结构。
无比逻辑:

逻辑电平和器件的尺寸无关。故而可以采用最小的尺寸：$L=2\lambda$
稳态下有限的（低）的输出电阻

稳态输出时，输出和VDD或GND之间用于存在一条有限电阻的通路，使他对噪声不敏感
高的输入电阻
- 输入是从栅极输入，栅极电流几乎为零，故而电阻极高
- 因为极低的栅极电流，故而理论上，一个INV可以驱动多穷多个INV。但是由于栅极寄生电容的原因，过多的扇出会使得输出电容$C_L$过大，使得$t_p$过高，动态特性变差。
稳态的下，无$I_D$电流——无功耗

稳态条件下，互补CMOS中始终有一个”开关“打开，故而没有电流的存在，意味着没有静态功耗

3. VTC（电压传输特性）

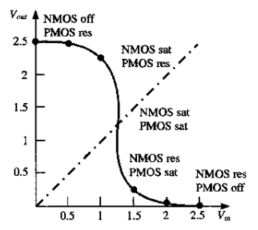
所有的工作点不是输出高电平就是输出低电平，如下图：

静态CMOS反向中PMOS和NMOS的负载曲线，原点表示直流工作点

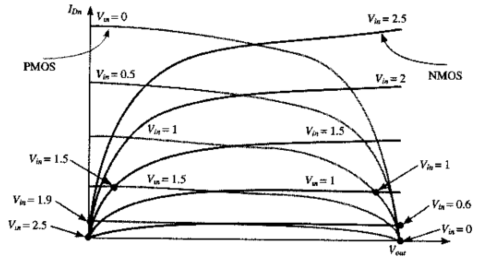
过渡区的电平范围很窄，如下图：

3. INV的静态特性

1. 开关阈值（$V_M$）

定义：$V_M$被定义为$V_{in}=V_{out}$的点。对于INV而言，此时$V_{GS}=V_{DS}$
结论：

$V_M≈\frac{rV_{DD}}{1+r}$

其中，r为PMOS与NMOS相对驱动强度之比

希望值：

$V_M=\frac{V_{DD}}{2}$

因为这样可以使得低电平噪声门限和高电平噪声门限的值相近，于是得到【r应该尽可能等于1】

经过推导，可以把$V_M=\frac{V_{DD}}{2}$映射为PMOS管和NMOS管的W之比，如下：

$\frac{(W/L)_p}{(W/L)_n}=\frac{W_p}{W_n}(数集中L相等)=...$

以下结论：

$V_M$对于器件$\frac{W_p}{W_n}$尺寸的变化不敏感。意味着工艺上的偏差，并不会使$V_M$偏差希望值很多。
增加$W_p$会使得$V_M$移向$V_{DD}$，增加$W_n$会使得$V_M$移向$GND$

2. 噪声门限

注：数集中，噪声容限都很大，接近$\frac{V_{DD}}{2}$，故而过度讨论他并没有太大的用处，此处仅作了解。

定义$V_{IH}$和$V_{IL}$分别是VTC中增益=-1的点。

定义噪声门限为：

$NM_H=V_{DD}-V_{IH} \\ NM_L=V_{IL}-0$

实际实验中，$NM_H$和$NM_L$并不完全相等，但是基本都可以到达1V左右，属于很大的噪声门限了。

3. 稳定性

器件参数变化对器件稳定性的影响：

仿真测试：PVT（process voltage temperature）：常常在设计中，采用三者组合仿真。
- 工艺角（process corner）分析，常见的五种：
1
2
3
4
5
fast nmos and fast pmos （ff） slow nmos and slow pmos （ss） slow nmos and fast pmos （sf） fast nmos and slow pmos （fs） typical nmos and typical pmos （tt）
1
2
3
t,代表typical (平均值) s,代表slow（电流小） f,代表fast（电流大）
- 电压（voltage）分析，常见的三种：
1
v+10% ,v ,v-10%
- 温度（temperature）分析，常见的四种
1
-40℃, 0℃,25℃, 125℃
在进行不同的组合，仿真最好最坏的等多种情况。

器件电源电压降低对器件稳定的影响

不可使用过低的电压
1. 低电压可以减小功耗（$P=C·V_{DD}^2$），但是会增加门延时。
2. 电源电压减低使得dc特性（开关阈值）对器件的尺寸越来越敏感。
3. $V_{DD}$减小，信号摆幅减小，有利于减小系统内部噪声。

4. 【重点】INV的动态特性——$t_p$（计算$R_{eq}$和$C_L$）

1. 设计角度

最小的传播延时

这是厂家最希望的
满足性能的同时，做到面积最小

面积最小，意味着成本最低。这里的面积取决于$W$，也就是选择合适的$W$
根据扇出设计反相器链的级数

对于时钟树、复位树等需要多扇出的、且要求$t_p$小的，如何设计一个合理的高扇出的反相器链
输入信号的上升下降时间对传播延时的影响

2. 计算$C_L$

$C_L=晶体管的漏极电容+连线电容+扇出门的输入电容$

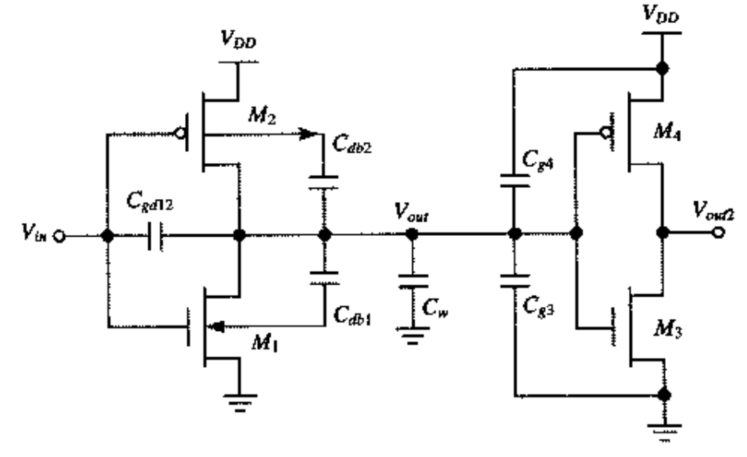
晶体管的漏极电容：$C_{db2}+C_{db1}+C_{gd12}$

即：两个管子的漏极电容，即管子1和2的结构电容总和$C_{gd12}$，管子1的结电容$C_{db1}$，管子2的结电容$C_{db2}$

其中，
1. 结构（覆盖）电容是固定的（有时候会使用密勒效应）：$C_{gd12}=2C_{gdo}=2C_oW$
2. PN结电容：$C_{db}=C_{diff}=C_{bottom}+C_{sw}$；或者使用线性化的值：$C_{eq}=K_{eq}C_{j0}$（推导见P55）
连线电容

与连线的长度、宽度，扇出门离驱动门的距离、扇出门的数量有关。
扇出的栅电容：$C_{g3}+C_{g4}$

即：两个扇出CMOS管的栅极电容。

而栅极电容具体看前文，1个CMOS管的栅极电容=2个结构电容+3个沟道电容

3. 等效电阻$R_{eq}$

$R_{eq}=\frac{1}{V_{DD}/2}\int_{V_{DD}/2}^{V_{DD}}\frac{V}{I_{DSAT(1+\lambda V)}}dV≈\frac{3}{4}\frac{V_{DD}}{I_{DSAT}}(1+\frac{7}{9}\lambda V_{DD})$

具体推导见书本P70

4. 【※重要】计算延时$t_p$——计算、优化

$t_{pHL}=0.69R_{on}C_L\\$

使用等效$R_{eq}$，则

$t_{pHL}=0.69R_{eqn}C_L\\ 同理，t_{pLH}=0.69R_{eqp}C_L$

上面两个值不一定相等！！

故，

$t_p=\frac{0.69(R_{eqn}+R_{eqp})C_L}{2}$

又经过一波推导，得出

$t_{pHL/LH}\varpropto \frac{C_L}{(W/L)V_{DSAT}}$

故【减小延时的方法】

减小$C_L$
增加$(W/L)$。增加$W$也会使得$C_L$增加，故有一个增加的范围。
提高$V_{DD}$。会增加能耗，而且增加到一定程度之后优化的效果有限。

5. 根据【延时】设计电路

1. 对称反相器

如何得到对称反相器——调整宽长比

对称反相器常常用于时钟网络（CLKINV）中，其有以下几个特点：
1. 充电电流和放电电流相等
2. 上升延时时间$t_{pLH}$和下降延时$t_{pHL}$大致相等
3. 晶体管电阻$R_P=R_N$
在.25工艺中，要得到对称反相器，一般要求：

可以认为，设计一个对称反相器，其目标是使得上下两个MOS管匹配。然而，这并不意味着反相器有着最短的延时（性能不是最佳）

※ 其原因是较宽的$W_P$可以改善反相器的$t_{pLH}$（$W_P\uparrow ,R_P \downarrow ,t_{pLH} \downarrow $），但是会导致$t_{pHL}$增大（$W_P\uparrow ,C_L \uparrow ,t_{pHL} \uparrow $）。如下图所示：

CMOS反相器延时和宽长比之比β的关系

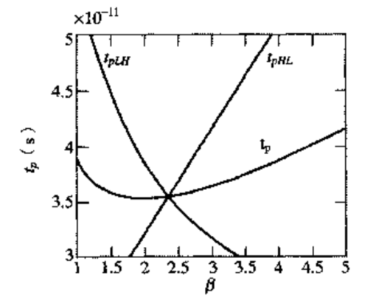
根据上图，我们可以知道，在$\beta=2.4$时，得到对称反相器；而当$\beta=1.9$时，得到传播延时的最小值——性能最佳的INV。

如何根据【性能—负载】选择对称反相器的尺寸

计算延时的时候，我们利用公式：
$t_{p}=0.69R_{eq}C_L\\$
其中，令
$C_L=C_{int}+C_{ext}$
$C_{int}$表示反相器的本征输出电容，常常为（驱动管）$N$管和$P$管的漏电容。

$C_{ext}$：表示下一级反相器的输入电容，常常为（负载管）栅电容（忽略导线电容）。

引入参数$S$：尺寸系数，即该反相器的晶体管和最小晶体管尺寸之比。

如果P管和N管的$W$同时增大$S$倍，

本征电容$C_{int}$增大$S$倍
等效电阻$R_{eq}$减小$S$倍

经过推导（看书），有以下结论：
$t_p=t_{p0}·(1+ \frac{C_{ext}}{C_{int}})=t_{p0}·(1+ \frac{C_{ext}}{SC_{int-ref}})$
$C_{int-ref}$：最小尺寸的INV的本征输出电容，因为对于有一个反向器而言，本身的漏极电容是确定的，故称为本征输出电容。

$C_{int}$：（驱动管）$N$管和$P$管的漏电容。

$C_{ext}$：（负载管）栅电容（忽略导线电容）。

$t_{p0}$：本征延时——尺寸变化$S$倍，则$R \rightarrow R/S,C \rightarrow SC$，如果令$t_{p0}=0.69RC$，则 $t_p=0.69·R/S·SC=t_{p0}$

反相器的本征延时和门尺寸无关，但是外界负载电容会导致影响反相器的传播延时
适当增加$S$可以减弱外界负载的影响。$S\rightarrow \infty ，\frac{C_{ext}}{SC_{int-ref}} \rightarrow 0$，此时$t_p=t_{p0}$

一般而言，S=5已经可以改善外界负载带来的延时，S>10之后收益很小。$S$增加过多之后，会导致面积变得非常大，然而电容减低不多。

$eg$：

假如某反相器的本征输出电容值$C_{int-ref}=1$，外部电容$C_{ext}=100$，而因为本征延时$t_{p0}$与尺寸无关。故而如果把尺寸增加5倍，即$S=5$，就可以把延时从$101t_{p0}$降为$21t_{p0}$，相当于延时降低了5倍。

2. 性能最好（$t_{p-min}$）的反相器

上面可以知道对称反相器并不是最佳的反向器，如何调整宽长比之比$\beta$得到最佳性能的反相器？

最佳性能INV的宽长比之比满足

$\beta = \sqrt{r}$

其中，$r$为P管和N管尺寸相同时的电阻比，即

$r=\frac{R_{eqp}}{R_{eqn}}$

最佳性能的INV需要以对称性和噪声容量为代价。如上图，$\beta = 1.9$时，得到性能最佳的INV。

3. 反相链的设计

反相链结构图：

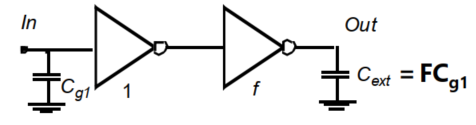
假设此处的反相链是由对称反相器构成的，根据对称反相器的延迟公式：

$t_p=t_{p0}·(1+ \frac{C_{ext}}{C_{int}})$

如果令

$C_{int}=\gamma C_g\\ C_{ext}=f C_g\\$

这里的$C_g$指的是驱动管的栅极输入电容（对比上文的几个电容。$C_{int-ref}$指最小尺寸驱动管的输出电容；$C_{int}$指驱动管的输入电容，其大小是$SC_{int-ref}$；$C_{ext}$指驱动管的输入电容和线电容，这边$C_g$并没有要求是最小尺寸）；$\gamma $：比例系数，只与工艺有关；$f$：等效扇出，即第$j+1$级管子相对于第$j$级管子的尺寸。

于是，可以得到

$t_p=t_{p0}·(1+ \frac{f}{\gamma})$

经过推导，要让反相链的延时最短，第$j$个反相器需要满足

$C_{g,j}=\sqrt{C_{g,j-1}·C_{g,j+1}}$

如果要达到这个，需要满足第$j$级的反相器尺寸永远是第$j-1$级反相器尺寸的$f$倍（前文提到，令$C_{ext,j+1}=C_{g,j+1}=f C_{g,j}$，故而只有满足$C_{g,j}=\sqrt{C_{g,j}/f·fC_{g,j+1}}$，等式才永远成立。）。

对于由$N$个反相器组成的反相链，可以得到

$f=\sqrt[N]{C_{ext}/C_{g1}}=\sqrt[N]{F}$

其中，$F$为总等效的扇出，$F=C_{ext,N}/C_{g,1}=C_{g,N+1}/C_{g,1}=C_L/C_{g,1}$（忽略导线电容）

【总结】：反相器链中，每个反相器尺寸都是前一个反相器的$f$倍，则说明每一级反相器拥有相同的等效扇出（等效扇出就是$f$），并且有相同的延时，链总延时最小。

【公式总结】：

链的总延时：

$t_p=Nt_{p0}·(1+ \frac{\sqrt[N]{F}}{\gamma})$

其中，$N$为反相链链数；$F$为总等效的扇出，$\gamma$为比例系数，只与工艺有关。

$N$大，则反相器本身延迟$t_{p0}$占主导，需要降低本征延时$t_{p0}$

$N$小，则反相器的扇出占主导，应该适当降低每一级反相器的等效扇出$f$——经过推导，一般$f=3\sim4$

6. 功耗

1. 功耗组成

动态功耗：

来源于电容充放电
短路电流：

当输入电压在某一个区域时，使得上下两管同时导通，从而形成短路电流。
漏电流：

属于静态功耗

2. 动态功耗

1. 工作过程——能量分配

来源于电容充放电

充电：P管导通，N管截止

能量分配——从电源摄取能量：$EV_{DD}$：
- 充电过程，P管消耗能量：$\frac{1}{2}EV_{DD}$
  
  注意：此处P管消耗的功耗，和P管的尺寸无关
- 充电结束，电容$C_L$存储能量：$\frac{1}{2}EV_{DD}$
放电：N管导通，P管截止

能量分配——电容$C_L$存储的能量：$\frac{1}{2}EV_{DD}$
- 放电过程，N管消耗能量：$\frac{1}{2}EV_{DD}$

2. 公式

定义：每一次开关周期（由低到高，再由高到低）所需要的固定能量，即动态功耗。为

$E_{dyn}=C_LV_{DD}^2$

于是，定义每秒的平均动态功耗大小为

$P_{dyn}=C_LV_{DD}^2f_{0 \rightarrow 1}$

其中，$f_{0 \rightarrow 1}$为这个门电路每秒通断的次数，称为开关活动率

3. 如何降低功耗

从上文的公式中，可以得到动态功耗同三个参数有关。

降低电源电压。电源电压太低，电路性能会变差到难以接受。
减少反转率。逻辑和结构层次实现——en信号+与门
减少电容。考察$C_L$的组成（见上文），主要在于减少器件的尺寸

3. 短路电流引起功耗

1. 公式

每个开关周期消耗的能量：

$E_{dp}=t_{sc}V_{DD}I_{peak}$

每秒平均功耗为

$P_{dp}=t_{sc}V_{DD}I_{peak}f_{0 \rightarrow 1}$

其中，

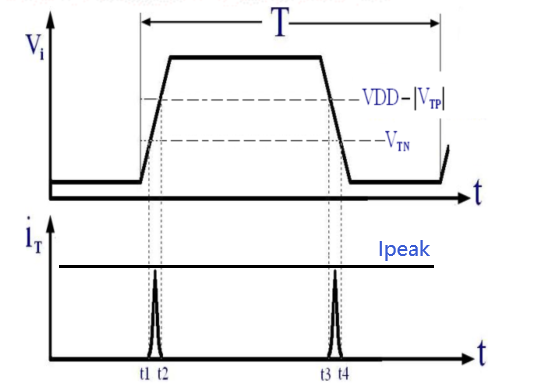
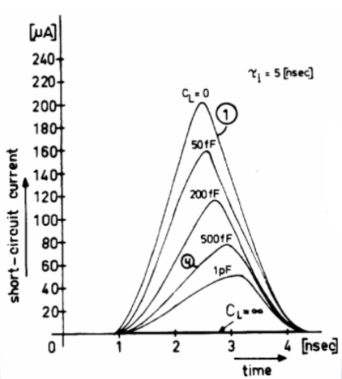
$t_{sc}$：上下两管同时导通的时间，如下图中的$t_2-t_1$和$t_4-t_3$。当输入信号大小满足$V_{TH}<V_{in}<V_{DD}-|V_{TH}|$，两个管子同时导通。

$I_{peak}$：短路电流峰值大小，如下图。

$f_{0 \rightarrow 1}$：开关活动率。

2. 同负载电容$C_L$的关系

$C_L$很大

特征：输出下降时间>输入上升时间

结果：输入在输出改变之间已经通过了过渡区（指$V_{TH}<V_{in}<V_{DD}-|V_{TH}|$），此时短路电流小

电路功耗：主要来自动态功耗。
$C_L$较小

特征：输出下降时间<输入上升时间

结果：输入在输出降到0还在过渡区，此时PMOS管漏-源电压近似为$V_{DD}$，此时短路电流极大。

电路功耗：主要来自短路电流

负载电容大小与短路电流的关系

4. 静态功耗（漏电流）

1. 公式

$P_{stat}=V_{DD}I_{stat}$

其中，$I_{stat}$为没有开关活动时，电源两条轨道之间流动的电流。

2. 组成部分

静态功耗主要组成

亚阈值漏电功耗
PN结漏电功耗

5. 总结

$P_{tatol}=P_{dyn}+P_{dp}+P_{stat}$

其中，

动态功耗$P_{dyn}$：主导位置。

短路电流功耗$P_{dp}$：可以经过把控$C_L$的大小，把功耗控制在限定的范围之内。

静态功耗$P_{stat}$：正在变得与来越重要。

7. 利用【功耗】设计电路

这边主要利用【动态功耗】设计【反相器链】

设计目的：使整个电路功耗最小，且满足最低性能要求。

可变的设计参数：反相器等效扇出系数$f$（后级反相器与前级反相器尺寸比）、电源电压$V_{DD}$

设计目标：延迟不大于参数为$f，V_{DD}=V_{ref}$的参考电路

考虑降低电压

①随着$f$的增加，电路的性能有所增加，此时可适当降低电源电压$V_{DD}$

②当$f$满足，

$f=\sqrt{F}$

得到最理想的尺寸系数。此时，电源电压可以降到最低。

PS：当$F=1$时，$f=1$是最好的情况，如下图。

③当$f>\sqrt{F}$，器件本征电容增加，性能降低，此时需要提高电源电压。

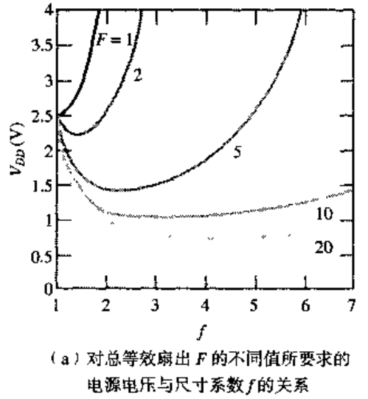
【小贴士】：延迟最低的等效扇出系数为$f=\sqrt[N]{F}$

《数字集成电路》课程笔记

数字IC基础

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

数字集成电路（4）CMOS组合逻辑门电路上一篇

数字集成电路（2）MOS晶体管下一篇

数字集成电路（3）反相器

第五章 反相器

1. 设计指标

2. INV综述

1. INV的数集模型

2. INV的特性综述

1. 动态特性：

2. 静态特性：

3. VTC（电压传输特性）

3. INV的静态特性

1. 开关阈值（$V_M$）

2. 噪声门限

3. 稳定性

4. 【重点】INV的动态特性——$t_p$（计算$R_{eq}$和$C_L$）

1. 设计角度

2. 计算$C_L$

3. 等效电阻$R_{eq}$

4. 【※重要】计算延时$t_p$——计算、优化

5. 根据【延时】设计电路

1. 对称反相器

2. 性能最好（$t_{p-min}$）的反相器

3. 反相链的设计

6. 功耗

1. 功耗组成

2. 动态功耗

1. 工作过程——能量分配

2. 公式

3. 如何降低功耗

3. 短路电流引起功耗

1. 公式

2. 同负载电容$C_L$的关系

4. 静态功耗（漏电流）

1. 公式

2. 组成部分

5. 总结

7. 利用【功耗】设计电路

第五章反相器