数字集成电路(5)努力
本文最后更新于:2023年10月16日 晚上
本人《数字集成电路设计》课程笔记,老师为王仁平。
本文主要讲述静态互补CMOS电路“努力”计算,并且通过“努力”计算设计最佳逻辑链电路。
第六章 CMOS组合逻辑门电路
4. 【静态CMOS】组合逻辑的优化
1. 总论
不同材料工艺
CMOS、双极性、BiCMOS、GaAs、超导等材料
逻辑级优化
- 逻辑深度:流水线【一级变n级】
- 电路拓扑:逻辑电路寄存器放几个、怎么放、要不要放;重定时(主要EDA工具完成)
- 扇出
- 门的复杂性
电路优化
逻辑类型、晶体管尺寸、不同频率下的电路模型
物理优化
版图策略
布局布线
2. 【重点】努力
根据INV延时的通式,
推广到所有的逻辑电路中,即有
其中,
$t_{p0}$:简单INV的本征延时。
$p$:复合门和简单INV的本征延时之比(显然,INV的$p=1$)。
$g$:逻辑努力
$f$:电气努力,即讨论INV链时说的等效扇出,定义为$C_{ext}=f C_g$,第$j+1$级管子相对于第$j$级管子的尺寸。
$h$:门努力,即$h=g·f$
为了方便讨论,将反相器的延时作为单位,进行归一化,将所有逻辑电路的延时用反相器延时作为单位进行表示。
设定,一个标准的反相器(对称反相器),$W_P=2,W_N=1$,即$W_{INV}=3$,即一个单位的$W=3$
设定,
$g_{INV}=1$(一个标准的INV,其$W=3$)
$p_{INV}=1$(一个标准的INV,其本征延时为$t_{p0}$)
$\gamma=1$(一个标准的INV,其本征漏电容等于输入栅电容)
下面对上面的参数进行讨论
1. $p$(本征延时比)
如果忽略内部节点电容,$p$的计算:
因,$C_{int}=a·W$,于是电容值可以用$W$来代替。
注意,是和输出端相连的管子才参与计算
例子:
| 门类型 | $p$ |
|---|---|
| 反相器INV | $1$ |
| $n$输入的NAND 或 $n$输入的NOR | $n$ |
| $n$路多路开关 | $2n$ |
| XOR,NXOR | $n2^{n-1}$ |
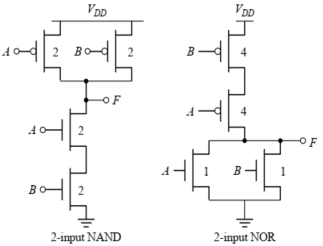
如上图,
对于2-input NADN,$C_L=C_{PB}+C_{PA}+C_{NA}=2+2+2=2·3$
对于2-input NOR,$C_L=C_{PA}+C_{NA}+C_{NB}=4+1+1=2·3$
忽略内部节点电容,也就是2-input NAND的两个NMOS管之间的电容、2-input NOR的两个PMOS管之间的电容忽略不计。
因为逻辑门的宽长比是按照标准INV(对称INV)的设定的,于是有$R_{PUN}=R_{PDN}=R_{INV}$
通过计算可知,
2. $g$(逻辑努力)和$G$(路径逻辑努力)
定义:一个门在最坏情况下,与反相器提供相同的输出电流(即电阻相等或驱动能力相等)时,所表现的输入电容比反相器大多少倍。
小贴士:
- 反相器有最小的逻辑努力
- 随着门的复杂度增加,逻辑努力相应增加
- 只和门的拓扑有关,与尺寸无关
逻辑努力$g$的计算:
| 门类型 | 1 input | 2 input | 3 input | n input |
|---|---|---|---|---|
| 反相器 | 1 | |||
| NAND | 4/3 | 5/3 | (n+2)/3 | |
| NOR | 5/3 | 7/3 | (2n+1)/3 | |
| MUL | 2 | 2 | 2 | |
| XOR | 4 | 12 |
例子:
对于2-input NADN,对于端口$A$,可知$C=C_{PA}+C_{NA}=2+2=4$,故$g=4/3$;端口$B$同理。
对于2-input NOR,对于端口$A$,可知$C=C_{PA}+C_{NA}=4+1=5$,故$g=5/3$;端口$B$同理。
对于路径逻辑努力$G$
对于一条路径,该路径的逻辑努力等于路径上所有门的逻辑努力连乘。
3. $b$(分支努力)和$B$(路径分支努力)
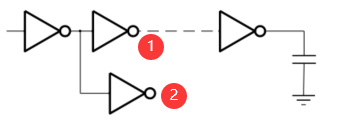
公式:
注意:
- 分支努力$b$是针对与一个路径节点而言的
- 如果只有一条路径,没有分叉,则$b=1$;如果该节点两个分支的栅电容大小相等,则$b=2$
其中,
- $C_{on-path}$:沿着分析路径上的负载电筒
- $C_{off-path}$:离开该路径连线上的电容
$eg:$假设,①反相器尺寸为2,②反相器尺寸为1,则$b=\frac{2+1}{2}=\frac{3}{2}$
对于路径分支努力$B$
对于一条路径,该路径的分支努力等于路径上所有节点的分支努力连乘。
4. $f$(电气努力)和$F$(路径电气努力)
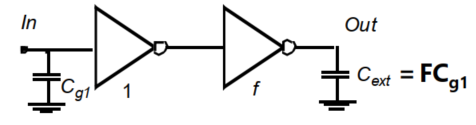
$f$又称为等效扇出,表示第$j+1$级管子($j+1$级输入电容)相对于第$j$级管子($j$级输入电容)的尺寸(电容值)。
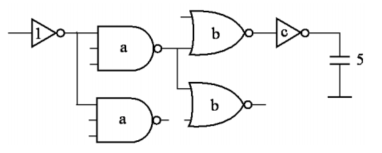
注意:对于第1级反相器和第2级两个3-input NAND,$f=\frac{2·C_{g-3-input-NAND}}{C_{g-inv}}$(3-input NAND尺寸相等,才能直接$·2$)
但是如果我们计算某一条路径,如上图所示分叉中某一路径,只针对路径上面的门电路计算电气努力
可知,
也就是算路径电气努力的时候(见下文),为何是$\prod\frac{f}{b}$
$F$为路径电气努力,又称为总等效的扇出,即最后一级的负载电容与第一级输入栅电容的关系。
经过推导(略),可知$F$又可表示为
对于一条路径,该路径的电气努力等于路径上所有门的电气努力连乘然后除以路径分支努力。
5. $h$(门努力)和$H$(路径门努力)
其中,
逻辑努力$g$,与拓扑(逻辑门类型,比如NAND、NOR等)有关,与具体尺寸无关。
电气努力$f$,即等效扇出。$f=C_{ext}/C_g$
注意,除以栅输入电容,而不是本征电容
$H$路径门努力公式如下:
$PS$:$H=\prod_{1}^nh_i=\prod_{1}^ng_i·f_i=\prod_{1}^ng_i·\prod_{1}^nf_i=G·\frac{\prod_{1}^nf_i}{B} ·B=GFB$
3.【重点】【优化】 确定电路尺寸
为了追求更好的性能,即最低的延时,我们希望可以调整尺寸,让组合逻辑的延时最小。
计算路径的总努力:$H=GFB$
确定路径上的门数:$N$
计算门努力:$h=\sqrt[N]{H}$
注意:经过推导,当$h$满足上式时,路径延时最短
根据$h_i=g_i·f_i$求出不同级门的尺寸$S_i$【尺寸系数$S$详见(3)4.3】
推导如下:
※本征延时和路径中逻辑门的类型有关,和尺寸无关。具体推导看(3)4.3
一个单位尺寸的门具有和最小尺寸反相器相同的驱动能力,即可知该门的输入电容$C_{j-in}=g_jC_{ref}$
若该门的尺寸系数为$S_j$,则该门的输入电容$C_{j-in}=S_jg_jC_{ref}$
根据上文4.2.3 可知,路径上面,
于是,
$eg:$求出路径上各级门的尺寸系数$S$

如上图电路图,可以将电路分成以下4级
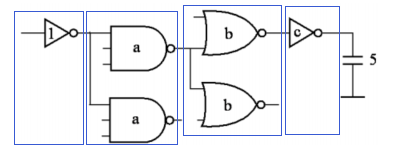
步骤一:确定$G、B、F$
由图可知,$C_L=5,C_{g1}=1$,故$F=C_L/C_{g1}=5$
接下来求解$G、B$
第1级:
第1级为一个反相器,即:$g_1=1$;
在输出节点,有两个分支,且两个分支尺寸相等,即:$b_1=\frac{1+1}{1}=2$
第2级:
第2级为两个尺寸相等的3-input NAND,即:$g_2=5/3$;
在输出节点,有两个分支,且两个分支尺寸相等,即:$b_2=\frac{1+1}{1}=2$
第3级:
第3级为两个尺寸相等的2-input NOR,即:$g_3=5/3$;
在输出节点,只有一条路径,即:$b_3=1$
第4级:
第4级为一个反相器,即:$g_4=1$;
在输出节点,只有一条路径,即:$b_4=1$
于是,有$G=1·\frac{5}{3}·\frac{5}{3}·1=\frac{25}{9}$;$B=2·2·1·1=4$
故$H=G·B·F=\frac{25}{9}·4·5=55.69$
| 第一级 | 第二级 | 第三级 | 第四级 | 总 | |
|---|---|---|---|---|---|
| $g$ | 1 | 5/3 | 5/3 | 1 | $G=25/9$ |
| $b$ | 2 | 2 | 1 | 1 | $B=4$ |
步骤二:确定级数$N$
由图可知,$N=4$
步骤三:计算门努力$h$
步骤四:计算尺寸系数$S_i$
已知:$S_1=1$
于是:
$S_2=\frac{h_{1}S_{1}}{b_{1}g_{2}}=\frac{2.73·1}{2·\frac{5}{3}}=0.819$
$S_3=\frac{h_{2}S_{2}}{b_{2}g_{3}}=\frac{2.73·0.819}{2·\frac{5}{3}}=0.671$
$S_4=\frac{h_{3}S_{3}}{b_{3}g_{4}}=\frac{2.73·0.671}{1·1}=1.832$
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!