数字集成电路(8)动态CMOS
本文最后更新于:2022年10月19日 下午
本人《数字集成电路设计》课程笔记,老师为王仁平。
本文主要讲述动态逻辑门的基本概念和多米诺逻辑。
第六章 CMOS组合逻辑门电路
9. 动态CMOS
静态CMOS:稳态时,通过低阻路径连接$V_{DD}$或$GND$
- 互补CMOS:上下网络互补,上拉到$V_{DD}$,下拉到$GND$。管子数为$2N$
- 传输管逻辑:上拉网络用其他代替,有比逻辑,存在$V_{TH}$。管子数为$N+1$
动态CMOS:依靠高阻抗上的电容存储临时的信号。管子数为$N+2$
1. 动态门
1. 综述
结构如下,
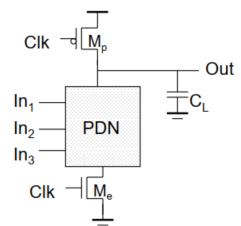
工作方式:工作分为两个阶段
- 预充电:$CLK=0$,$M_P$导通,对$C_L$充电
- 求值:$CLK=1$,$M_N$导通,$OUT$和$GND$之间存在低阻通路。
特点:
- 全电压摆幅
- 无比逻辑(同互补CMOS,异传输管逻辑)
- 噪声容限低。因为$out$在预充电阶段已经充电到$V_{DD}$,即$V_{DS}$已经满足$>V_{OV}$,于是只要$V_{IN}>V_{TH}$,管子就会导通。
- 需要预充电和求值的时钟。
- 较快的开关速度。原因如下,
- 相对互补CMOS,缺少了上拉网络的一个门,相对负载是互补CMOS,负载是动态门的$C_L$比较小
- 动态门没有短路电流(同一个时刻,只能一个$M$导通),由下拉网络提供的所有电流都用于$C_L$电容的放电(?)
- 如果$IN=0$,则不存在输出延时(预充电完输出即为1);如果$IN=1$,则需要$C_L$放电
- 晶体管重复利用,减小面积(多输出多米诺)
优点:
- 提高速度
- 减小面积(多输出多米诺;$N+2$个管子)
- 没有短路功耗
- 没有毛刺(因为一次只能翻转一次,$C_L$放电完只能等效下一次预充电才能回到1)
2. 存在的问题——信号完整性问题
电荷泄露
来源:与$C_L$相连的管子存在反偏二极管和亚阈值漏电。
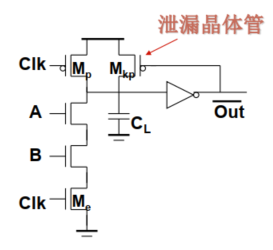
解决办法:使用泄露晶体管
- 反馈形式的伪NMOS型上拉器件。
- 该晶体管为了减小功耗和尺寸,一般选用尺寸较小(电阻值大)的管子。
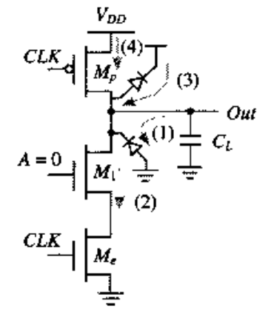
电荷分享
来源:下拉网络中存在的节点电容$C_A$。当$A=0→1、B=0$,则原本存储在电容$C_L$上的电荷在$C_L$和$C_A$之间重新分配,造成输出电压有所下降。
※需要满足$A=0→1、B=0$才能进行电荷分享,否则当$B=1$的时候,求值过程中($CLK=1$),$C_L$存储的电荷将全部被释放掉,不存在点电荷分享现象。
【重点】【计算】计算电荷分享对于输出电压的影响
根据的是电荷守恒
关于计算,会在后面详解
解决办法:使用泄露晶体管
这种方法几乎不用。会增加面积和电容。
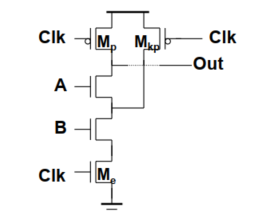
使用泄露晶体管$M_{kp}$对关键的内部节点预充电,但是会增加面积和电容。
注意:和上文中的“电荷泄露”中的泄露晶体管进行区分。
电容耦合(略)
使得$V_{out}$略有下降
时钟馈通(略)
起因:时钟输入和动态节点输出之间的耦合电容引起
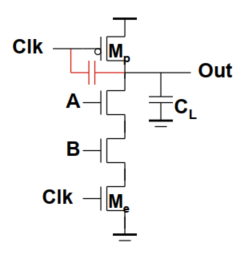
现象:时钟反转过快,则当$CLK$ $0\rightarrow 1$时,动态节点输出$>V_{DD}$;则当$CLK$ $1\rightarrow 0$时,动态节点输出$<0$
危害:时钟馈通危险在于可能使正常情况下反偏二极管变为正向偏置,导致出错
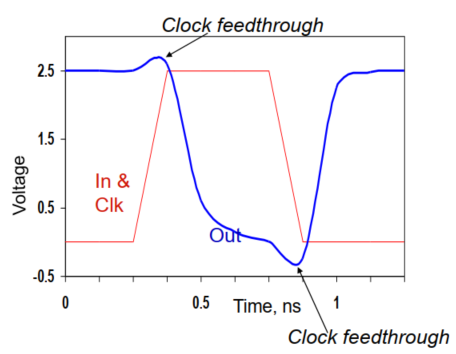
3. 【计算】计算电荷分享对于输出电压的影响
前提:没有加泄露晶体管的时候,电荷分享对于输出电压的影响
根据:电荷守恒定律
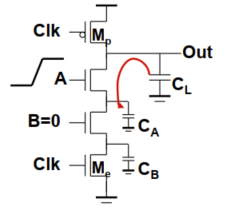
例1:
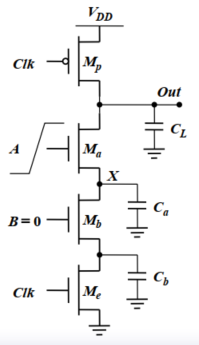
可知求值期间,$CLK=1$,因此电路如果存在电荷分享现象,则$A=1、B=0$才能存在电荷分享。
如果$A=B=CLK=1$,则$Out$对地有直接通路,则$C_L$的电荷将被全部放掉,不存在电荷分享的现象。
对于计算电荷分享,需要输出电压降$\Delta V_{out}$分两种情况:
首先假设其他参与电荷分享的电容上的电压和输出电压相等,即$V_{Cx}(t)=V_{out}(t)$
- $\Delta V_{out}>V_{Tn}$
- $\Delta V_{out}<V_{Tn}$
其中,
$\Delta V_{out}=V_{DD}-V_{out}(t)$。
$V_{DD}$为初始输出电压,因为$CLK=0$时输出预充电到$V_{DD}$
$V_{out}(t)$为电压分享之后的输出电压。
情况①:$\Delta V_{out}>V_{Tn}$,则实际上$V_{Cx}(t)=V_{out}(t)$
情况①:$\Delta V_{out}<V_{Tn}$,则实际上$V_{Cx}(t)=V_{DD}-V_{Tn}$
即电压分享之后,$C_L$上的电压或者说输出电压和其他参与电荷分享的电容上的电压相等。
因为$PDN$都是NMOS管,对于其他参与电荷分享的电容最多只能充电充到$V_{DD}-V_{Tn}$
如图中$X$点,当$A=1$时,即$V_{A}=V_{DD}$,则$V_X-max=V_{DD}-V_{Tn}$,因此$\Delta V_{X}(t)_{min}=V_{DD}-V_X-max=V_{Tn}$
因此如果$\Delta V_{out}>V_{Tn}$,则说明假设的参与电荷分享电容上的压降和$V_{DD}$之间的差值大于$\Delta V_{X}(t)_{min}$,满足假设
解题:
设$C_a=V_{out}$,则根据电荷守恒定律
计算得到$V_{out}$
根据$\Delta V_{out}=V_{DD}-V_{out}$和$V_{Tn}$的值
分为两种情况:
①$\Delta V_{out}>V_{Tn}$,则上面计算得到的$V_{out}$即为正确的值
②$\Delta V_{out}<V_{Tn}$,则
计算得到$V_{out}$
例2:
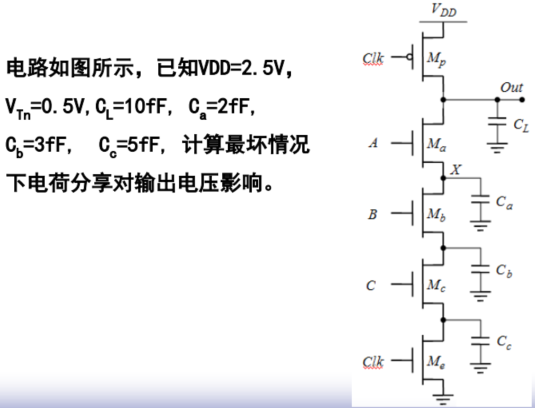
解题方法如上。
4. 串联动态门
存在的问题:前级的输出可能会影响到后级,从而使后级预充电完的$C_L$放电
解决办法:
规定预充电的时候,所有的输入均为0;当求值的时候,输入只能从0变化到1。
故在两级之间放一个
buffer(反相器)。当前一级预充电到1的时候,1经过反相器之后得到0,并且作为后一级的输入,确保预充电时所有的输入为0。
2. 多米诺逻辑
1. 综述
多米诺逻辑即为前文所述的串联动态门,目的就是保证预充电时,输入均为0;求值时,输入只做0→1的翻转
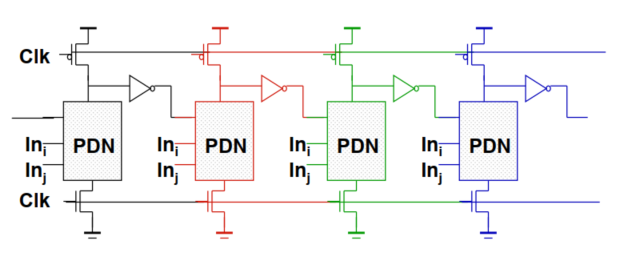
初始状态均为0,求值的时候根据前一级输出确定下一级输入,从而求下一级输出。
特点:
- 求值层层传播,如多米诺骨牌
- 求值阶段的时间取决于逻辑深度(因为求值时候的特性,见上)
- 只能实现非反向逻辑
- 无比逻辑
- 节点需要在预充电充完电,求值的过程中,输入需要特别稳定。
- 速度非常快(因为当上一级的输入都是0时,下一级相当于无延迟传播)
- 输入电容小(和互补CMOS比,只有一个管子)
2. 去掉下拉时钟网络
如下图所示,
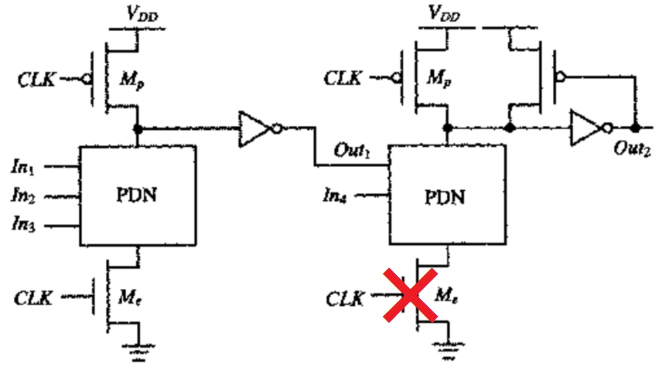
优点:
- 只需要第一级的下拉时钟负载,后面的不用。减少时钟负载。
- 速度和性能可以得到大大提升
缺点:
- 去掉下拉时钟网络,需要满足该动态门$CLK=0$时,该动态门输入均为0,否则可能导致短路
- 为了达到上文的目标,需要精确把控时钟。
方法:
不同级的动态门的$CLK$并不是同时的,需要逐级推迟时钟时间。
也就是该时钟必须通过逻辑网络传输,不同级之间可能需要Buffer进行缓冲延迟。这对于时钟的把控特别严格。
3. 多米诺逻辑的性能优化
调整反相器的晶体管尺寸
分析可知,
预充电过程中,主要经过两个门的延迟:
- $V_{DD}$通过上拉时钟PMOS管对$C_L$进行充电
- 本级动态门输出逻辑1经过反相器(INV的PMOS管)输出逻辑0,作为下一级输入
求值过程中,如果存在该动态门输入存在从$0→1$跳变,主要经过两部分延迟:
- 本级动态门下拉网络对$C_L$进行放电
- 本级动态门输出逻辑0经过反相器(INV的PMOS管)输出输出逻辑1,作为下一级的求值输入
可根据情况进行反相器尺寸的调整(一般为了减低求值时间,会增大INV的PMOS尺寸)
面积优化
采用多输出多米诺逻辑,见下文。
多输出多米诺逻辑中,动态逻辑门可以实现多种逻辑,可以重复利用一些晶体管,使得晶体管数目减小。
或者使用组合多米诺逻辑,见下文。
组合多米诺逻辑,并不需要在每个动态门之后加反相器,而是借助一个复合互补CMOS门将多个动态门组合起来。
4. 多输出多米诺
多输出多米诺可以重复利用一些晶体管,一个复合逻辑门里面可以实现多种逻辑,减小了晶体管数量,大大减小面积。
$eg$:
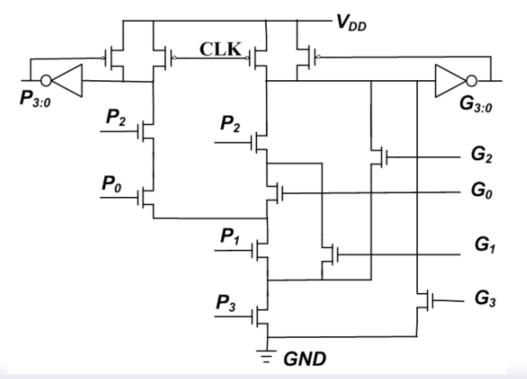
如上图所示,$P_{3:0}$和$G_{3:0}$共用$P_1$、$P_3$管子。
其中,$P_{3:0}=P_0P_1P_2P_3$;$G_{3:0}=G_3+$
5. 组合多米诺逻辑
组合多米诺逻辑,并不需要在每个动态门之后加反相器,而是借助一个复合互补CMOS门将多个动态门组合起来。
graph LR
动态门1 ==Y1==> 复合CMOS门
动态门2 ==Y2==> 复合CMOS门
动态门... ==Y...==> 复合CMOS门
复合CMOS门 ==> 结果
$eg:$
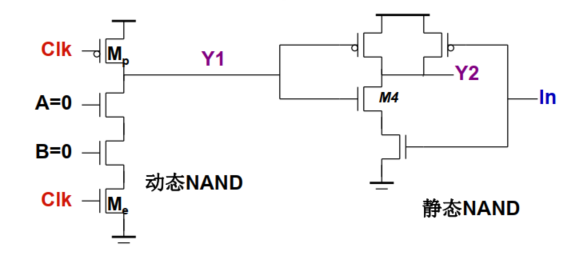
如上图,动态门组成逻辑:$Y1=\overline{A·B}$;经过静态互补CMOS门,组成逻辑$Y2=\overline{Y1·In}$
注意,$Y1$结果并不需要经过反相器
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!