数字集成电路（9）时序逻辑电路设计

本人《数字集成电路设计》课程笔记，老师为王仁平。

本文主要讲述时序电路中的基础元件：锁存器、寄存器（触发器）、施密特触发器。

第七章 时序逻辑电路设计

1. 时序电路的相关概念

1. 时序电路

框架：

结果：取决于当前的输入和过去的状态。

2. 静态/动态存储器

  1. 静态存储器：

    • 上电就保持存储状态

    • 通过正反馈，有意将输入和输出连接

    • 如果长时间不用可以用门控时钟关闭（起到降低功耗的作用）

      静态存储器（以正锁存器为例）

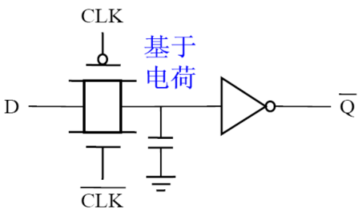
  1. 动态存储器：

    • 简单而言，即传输门+反相器，如下图。

    • 利用寄生电容存储高低电平

    • 只能存储较短的时间（$ms$级别）（电容小等原因使得存储时间短）

    • 需要周期性刷新来补偿泄露电荷（参见（8）动态门）

    • 结构简单，有较高性能（管子少，$RC$​小）和较低功耗（不存在静态功耗）

      image-20211010164426948

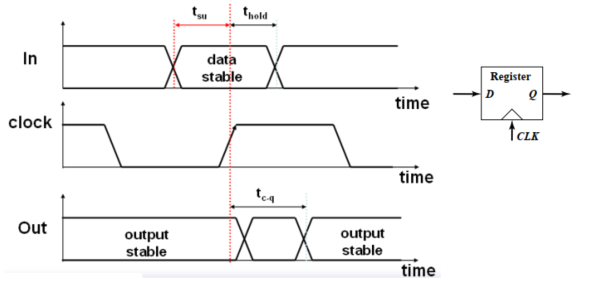
3. 时序参数

  1. 建立时间$t_{Setup}$​

    输入数据$D$在时钟有效沿到来前，必须有效的时间

  2. 保持时间（维持时间）$t_{Hold}$​​

    输入数据$D$在时钟有效沿到来之后，必须保持稳定的时间

  3. 传播时间$t_{Propagate\ Time}$​

    当满足建立时间和保持时间时，数据从输入端复制到输出端所需要的时间（$50\%$对$50\%$）。

    即时钟$CLK50\%$对输出端数据$50\%$​​，如下图。

为何这么说？

因为只有当满足了建立时间，此时时钟$CLK$​​​​才可以翻转，即此时的数据才是输入端输入的数据

所以输入端数据的$50\%$即为时钟的$50\%$

D触发器的建立时间、保持时间、传播时间

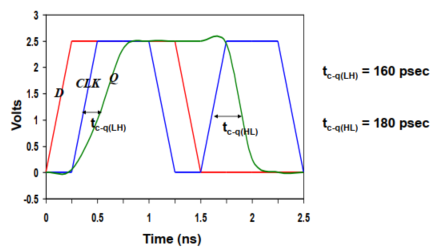
仿真实例中的传播时间（CLK50%对输出端数据50%）

小贴士：

  1. 建立时间$t_{su}$和保持时间$t_{hold}$​​​都是​针对时钟的有效沿而言的。

    即，输入数据$50\%$的时间对时钟有效沿$50\%$的时间；对于传播延时$t_{c-q}$，输入信号$50\%$（即时钟信号$50\%$）时间对输出信号$50\%$时间

4. 时序约束条件

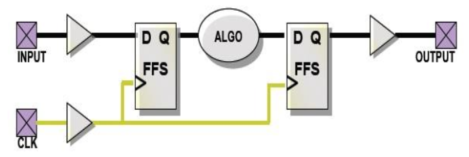
image-20211010170652507

  1. 时钟周期$T$​

    只有当当前所有计算全部完成，系统闲置，下个时钟（即下一个操作）才可到来。

    其公式如下，

    其中，

    $t_{c-q}$：时序电路的传播时间（图中为D触发器的传播时间）

    $t_{p-logic}$​：组合逻辑的最坏传播延时（图中为$ALGO$​的传播延时）

    $t_{su}$​：时序电路的建立时间（图中为D触发器的建立时间）

  1. 保持时间$t_{hold}$

    保证数据可以在有效沿保持足够长的时间，不会因新进入的数据而过早改变

    其公式如下，

    其中，

    $t_{hold}$：保持时间

    $t_{cd}$​：最小传播延时/时间，又称为污染延时，于是有

    $t_{cdreg}$：寄存器的最小传播时间

    $t_{cdlogic}$​：组合逻辑的最小传播延时

5. 锁存器和寄存器

项目 锁存器 寄存器
敏感类型 电平敏感
（有效电平内随意反转）		 边沿敏感
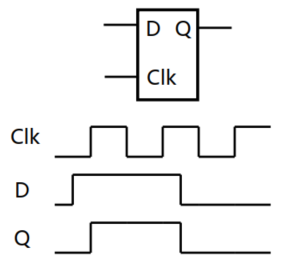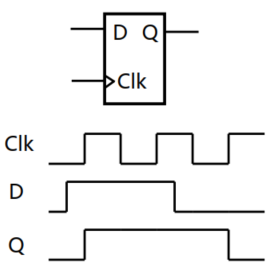波形 image-20211010194213324
波形解释 图为正锁存器。
当$CLK=1$，$Q=D$（透明模式）
当$CLK=0$，$Q=Q$（保持模式）		 图为上升沿有效D触发器
上升沿到来，$Q=D$
其他时候，$Q=Q$
需要注意的边沿
（该边沿到来需要考虑建立时间保持时间）		 正锁存器：时钟下降沿
负锁存器：时钟上升沿		 有效沿
备注 由锁存器作为基本单元构成

2. 静态锁存器/寄存器

1. 静态锁存器

1. 电路图与分析

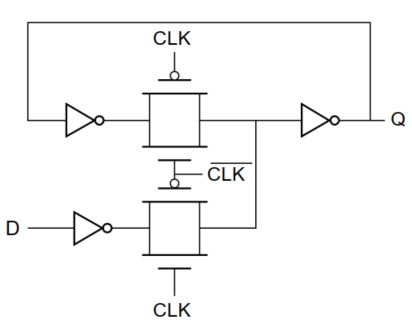
以正锁存器为例，电路图如下，

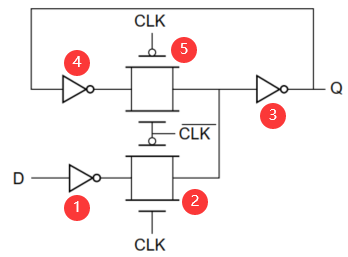
正锁存器电路图

电路结构：以传输门为主体的二选一选择器；$CLK=1$，$Q=D$；而$CLK=0$，通过正反馈，输出端和输入端连接。

2. 时序参数分析

1.5中提到，分析正锁存器时，需要注意的时钟边沿是时钟的下降沿。

这是因为，在$CLK=1$时，$Q=D$​，属于透明传输，即输出随输入随时变化。其信号传播路径：D-①-②-③-Q

当$CLK=1→0$时，锁存器将要对输入数据进行所存。因此需要考虑建立时间$t_{su}$​。

如果要让数据可以正确锁存下来，需要④⑤之间的节点的电平等于③⑤之间节点的电平，即

即，如果要所锁存数据A，则当数据A到达④⑤节点之前，$D=A$​​不可以改变，其信号传播路径：D-①-②-③-④-$Node_{④⑤}$​​

2. 静态寄存器——边沿触发寄存器

边沿触发寄存器，又称主-从寄存器，由主、从两个锁存器组成

1. 电路图与分析

框架图

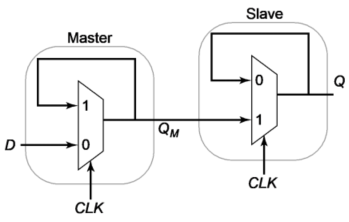
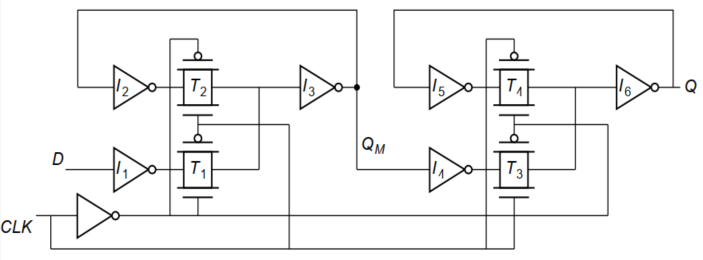
传输门电路原理图

时序图

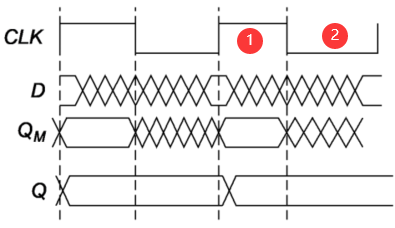
主-从寄存器，由主锁存器——负锁存器、从锁存器——正锁存器组成。

  • $CLK=0→1$​​​​​时，主锁存器锁存数据。
  • 在①阶段，即$CLK=1$，主锁存器输出$Q_M$保持不变，从锁存器随主锁存器输出值$Q_M$而变化（就是不变、从锁存器透明传输）；
  • $CLK=1→0$时，从锁存器锁存数据。​
  • 在②阶段，即$CLK=0$​​，​​​从锁存器持续输出锁存的数据。
过程总结
$CLK$ $0→1$（上升沿） 阶段①：$CLK=1$ $1→0$（下降沿） 阶段②：$CLK=0$
主锁存器 锁存数据 保持锁存 透明传输
从锁存器 透明传输 锁存数据 保持锁存

于是，有以下结论：

  • 寄存器的有效沿同从锁存器的敏感电平相关。对于从锁存器，如是正锁存器，则为上升沿；反之，下降沿。
  • 从锁存器可以持续输出一个值长达一个时钟周期。

2. 时序参数分析

传输门电路原理图

设定反相器延时为$t_{pd-inv}$，传输门延时为$t_{pd-tx}$​，时钟INV无延时。

明确：有效时钟沿为上升沿，一切参数均以有效时钟沿作为基准

1. 建立时间$t_{su}$

类似于2.1.2 静态锁存器时序参数的分析，可知需要满足$D_{I2-T2}=D_{T2-I3}$

即信号传输到$Node_{I2-T2}$之前，输入数据$D$​不能变化，数据路径为$D-I_1-T_1-I_3-I_2$​（3个INV，1个TX）

即有

2. 保持时间$t_{hold}$

当$CLK=1$时，$T_1$就会关断，因此需要保证$CLK=1$之前，数据$D$已经通过传输门$T_1$

因为数据$D$​进入$T_1$之前需要经过$I_1$；而时钟作用于$T_1$之前，同样需要经过$INV$​​；故而二者作用域于$T_1$时间差不多。

于是只需要留一定的余量给$t_{hold}$即可，即有

3. 传播时间$t_{c-q}$

前面1.3提到，传播时间是满足建立时间和保持时间之后，数据从输入端到输出端的时间（$50\%$​对$50\%$​）或者时钟$CLK50\%$对输出端数据$50\%$的时间（原因见1.3）。

满足了建立时间，此时输入数据$D$​​​已经到达了$Node_{I4-T3}$​​​（因为为了满足建立时间，数据到达$Node_{I3-I4}$​​之后，还要经历$I_2$​​。经历$I_2$​​的延时同数据经历$I_4$​​的延时相互抵消了）

此时传播时间即为$Node_{I4-T3}$​到达$Q$​的时间

而又因为此时$CLK=1$，从锁存器处于透明模式，故数据路径为$Node_{I4-T3}-T_3-I_6-Q$​（1个INV、1个TX）

即有，

3. 寄存器复位——同步/异步

1. 同步复位（RST=0时复位）

同步复位

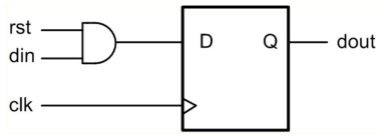
2. 异步复位（clr=0时复位）

异步复位

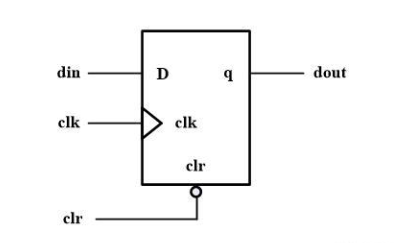
3. 动态锁存器/寄存器

1. 动态锁存器

电路图：

动态锁存器电路图

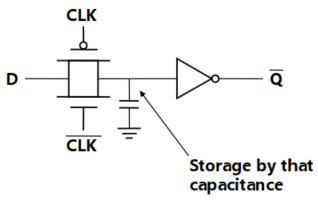
使用电容电荷表示一个逻辑信号。

但是值的保存时间有限（$ms$）（漏电时间），需要周期性进行刷新。

2. 动态寄存器

1. 电路图

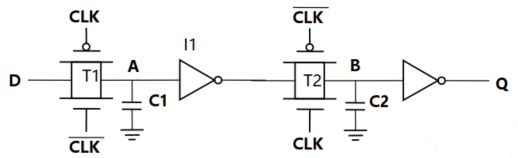
动态锁存器电路图

2. 工作原理：

$CLK=0$，$T_1$导通，$A$对$D$进行采样，并通过$C_1$充放电进行保存。

$CLK=1$​，$T_1$​关端，$T_2$​导通，从$A$​看$T_1$​和反相器$I_1$都呈现高阻态，$C_1$无法充放电，于是$C_1$​电荷值锁存。根据$D_A$​值，反相器$I_1$​进行对数据进行反向（即$I_1$​输出端上拉或者下拉），实现$C_2$​的充电或者放电。

$CLK=0$​​，$T_1$​​导通，$A$​​对$D$​​进行采样，并通过$C_1$​​​充放电进行保存。此时$T_2$​​截止，从$B$​​看$T_2$​​​和反相器$I_2$​都呈现高阻态，于是$C_2$​​只能保持电荷。

….

3. 时间参数分析：

  • 建立时间$t_{su}$​：

    输入信号$D$传输到$A$，并且$A$节点完成$C_1$​充电或放电时间（电容容值小，电荷量小，充电放电时间极短，可忽略不计）。

  • 保持时间$t_{hold}$：

    传输门在时钟边沿关断，近似0。

  • 传播延时$t_{c-q}$：

    满足建立时间和保持时间之后，此时信号已经到$A$​节点。传播延时（时间）即为信号从$A$到$Q$的时间。

    即2个反相器+1个传输门+$C_2$​​充放电时间。

4. 存在的问题

  1. 通过$C_1$、$C_2$​​​电容进行存储，抗干扰能力差（噪声容限低）。

  2. $C_1$、$C_2$​电容存在漏电现象，需要不断刷新。

  3. 时钟重叠问题：

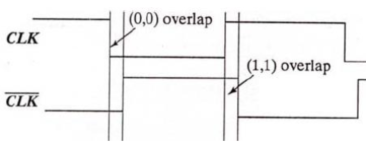
    时间重叠问题

$\overline{CLK}$是通过$CLK$反相而来，于是需要用到反相器，于是$CLK$和$\overline{CLK}$之间存在延时。

于是在时钟跳转的时候，二者会有一段时间电平相当，这样子工作是有问题的，即存在竞争行为。

解决办法：

  1. （0，0）重叠：PMOS均导通，需保证在$D$输入和节点$B$（数据不会影响到$C_2$电平）之间有足够的延时，以使主级采样的新数据不会传送到从级。
  2. （1，1）重叠：NMOS均导通，需要强加一个保持（维持）时间，使得$D$保持一段时间不变，即可。

5. 优化——提高噪声容限

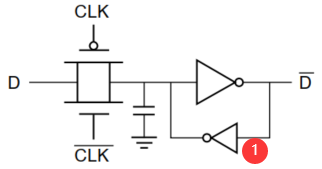
image-20211011170957239

增加弱反馈——反相器$I_1$​，形成“伪静态电路”​​，可提高抗噪能力。

缺点：增加少量延时。

4. 流水线和多周期路径

1. 流水线

电路的工作速度取决于时序电路间的组合逻辑

  • 可以通过将复杂、延迟大的组合逻辑（如计算$lg(A·B)$​）通过寄存器进行分割，提高做工效率。
  • 需要注意时序设计。每增加一个寄存器，结果就落后一拍！

2. 多周期路径

主要是写RTL代码时需要注意。

如果一个组合逻辑计算需要多个时间周期完成，可以通过一个cnt进行移位（移位运算量小）。当满足某个条件时，寄存器en=1，输出结果。

如：某运算需要经过四个周期完成，可以声明cnt=4'b0001，每个时钟进行左移，当cnt[3]==1'b1时，en=1，输出结果。

5. 双稳态时序电路

1. 施密特触发器

符号：

施密特触发器符号

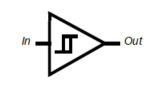
波形：

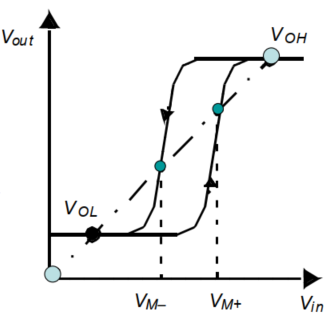
施密特触发器波形图

用处：将含有噪声或者缓慢变化的信号转变为一个干净的数字输出信号，即“0”或者“1”。

​ 或者说：抑制信号的振荡，使输入信号迅速翻转。

原理：一般采用互补CMOS进行搭建，改变PMOS管和NMOS管的$W$之比，实现$V_M$的改变。

​ （增大PMOS管的尺寸，$V_M$​​后移）

施密特触发器互补CMOS电路图

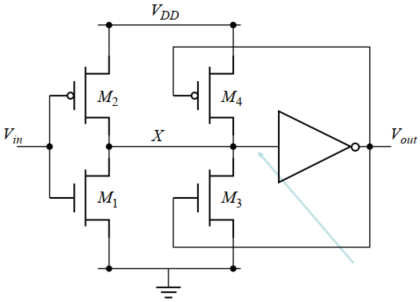
施密特触发器互补CMOS电路图

分析：

  1. $V_{in}=0→1$​​​，故最初，$V_{out}=0$​​，此时下拉网络$M_1$​​导通、上拉网络$M_2$​​、$M_4$​​​导通，即$\frac{W_P}{W_N}$增大，$V_M$​​​往后移。

    当$V_{in}>V_M$之后，则$M_4$截至而$M_3$导通，此时$\frac{W_P}{W_N}$减小，于是$X$信号可以加速$1→0$的翻转，从而可以得到高速翻转的$V_{out}(0→1)$

  2. $V_{in}=1→0$​，故最初，$V_{out}=1$​，此时下拉网络$M_1$​、$M_3$​导通、上拉网络$M_2$​导通，即$\frac{W_P}{W_N}$​减小，$V_M$​往前移。

    当$V_{in}<V_M$之后，则$M_3$截至而$M_4$导通，此时$\frac{W_P}{W_N}$增大，于是$X$信号可以加速$0→1$的翻转，从而可以得到高速翻转的$V_{out}(1→0)$