数字集成电路(4)CMOS组合逻辑门电路
本人《数字集成电路设计》课程笔记,老师为王仁平。
本文主要讲述静态互补CMOS电路基本概念和延时计算。
第六章 CMOS组合逻辑门电路
1. CMOS电路的分类
静态互补CMOS电路
即常见的CMOS电路——开关模型=理想开关+有限电阻
门输出通过一个低阻连接到$V_{DD}$和$GND$,输出为该电路实现的布尔值(0或者1)
特点如下:
- 高噪声容限(见(3)噪声门限)。
- 高输入阻抗,低输出阻抗
- 静态功耗可忽略(见(3)功耗)
动态CMOS集成电路
信号暂时存储在高阻抗电路节点上面的电容上——$RC$大
特点如下:
- 门电路简单、速度快
- 设计和制作工艺复杂
- 对噪声敏感
2. 静态互补CMOS设计
1. 何为互补CMOS
互补CMOS由上拉网络(PUN)和下拉网络(PDN)组成,每个输入都分配到上拉和下拉网络
如下图,以与非门为例:
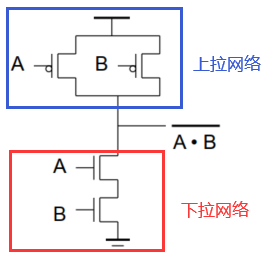
上拉和下拉网络是相互排斥的——上下只能同时一个导通
上拉:输出为1,$OUT$和$V_{DD}$之间存在通路
下拉:输出为0,$OUT$和$V_{SS}(GND)$之间存在通路
上拉:使用PMOS管,输出为强1,即$V_{out}=V_{DD}$;故一般使用PMOS管。
使用NMOS管,输出为弱1,即$V_{out}=V_{DD}-V_{THN}$
下拉:使用NMOS管,输出为强0,即$V_{out}=GND$;故一般使用NMOS管
使用PMOS管,输出为弱0,即$V_{out}=|V_{THP}|$
其原因在于:MOS管导通需要满足$V_{GS}>V_{TH}$
具有N输出的逻辑门所需的晶体管数为2N
2. 规则
以NMOS管作为分析对象,
即,NMOS管串联,实现与非功能;NMOS管并联,实现或非功能。
其关系如下图:
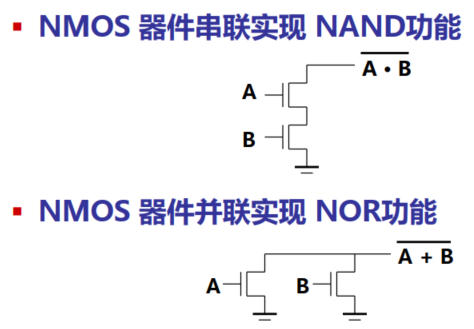
为何是非?
因为互补CMOS本身脱身于反相器,故自带非逻辑。
3. 设计复杂的逻辑门电路
1. 构成逻辑图的要素
- 网络节点:顶点
- 弧线:源-漏
- 弧线名:栅信号
2. 步骤
根据原理图画下拉网络——NMOS管构成
根据 串与并或的原则,画出下拉网络的逻辑图。
根据下拉网络,画出上拉网络(PMOS管)
- 每个闭合路径放置节点
- 设置节点:$OUT$、$V_{DD}$ 两个新节点
- PMOS管新弧线穿过NMOS管弧线,把节点连接起来
- 给定新的PMOS弧线和NMOS管弧线相同的逻辑标记
3. 【静态CMOS】分析逻辑门电路
CMOS管构成的电路分析,使用开关模型——理想开关+有限电阻+电容
以两输入与非门为例,如下图
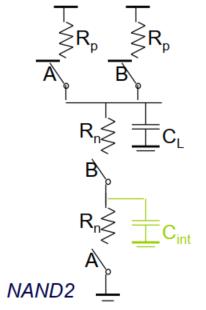
注意:有节点的地方,一般都有电容。如上图两输入与非门所示,两个串联的NMOS管之间存在节点,于是存在一个电容$C_{int}$;上拉和下拉网络之间存在节点,这个节点正好是输出结果的节点,为$C_L$
1. 【输入模式】影响互补CMOS的传播延时$t_p$
以两输入与非门为例,电路图如上图。
输出:低$\rightarrow$高
两个输入均→低 : 即通过两个上拉电阻对电容充电,上拉网络中两个管子导通。此时两个$R_P$并联
其中,$\frac{R_P}{2}$为两$R_P$电阻并联之后的电阻阻值。
一个输入为高,一个输入→低:即只通过一个电阻对电容进行充电,上拉网络仅有一个管子导通,此时只有一个电阻$R_P$
输出:高 $\rightarrow$ 低
- 两个输入均为高电平(或低→高):即通过两个下拉电阻对电容放电,下拉网络中的两个管子均导通。此时两个$R_N$串联其中,$2R_N$为两个$R_N$电阻串联之后的电阻阻值
此处给出一组表格。采用$NMOS=0.5\mu/0.25\mu;PMOS=0.75\mu/0.25\mu;C_L=100fF$
| 输入方式 | 延迟($ps$) |
|---|---|
| $A、B=0\rightarrow 1$ | 62 |
| $A=1;B=0 \rightarrow 1$ | 50 |
| $A=0 \rightarrow 1;B=1$ | 69 |
| $A=B=1 \rightarrow 0$ | 35 |
| $A=1;B=1 \rightarrow 0$ | 57 |
| $A=1 \rightarrow 0;B=1$ | 76 |
很明显,传播延时取决于输入模式
2. 【重点】如何确定晶体管尺寸
目的:使得做出来的逻辑门电路性能最好($t_p$最小)
指标:该逻辑门最坏情况下,与反相器提供相同的输出电流,即$R_{PUN-max}=R_{PDN-max}$。
即$t_{pHL}=t_{pLH}$。
相当于构建一个对称反相器
例子:
电阻大小和管子的$W$成反比
由于迁移率$\mu$的不同,此处我们认为,$W_P=2,W_N=1$时,管子有着相同的电阻。
这个系数$\frac{W_P}{W_N}=2$并不一定,根据工艺进行调整。
下面是版图上面的体现:
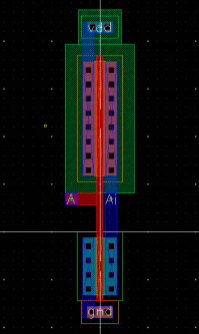
按照系数为2进行计算,即有
原因:PMOS管和NMOS管的$\mu$不同
注意:不同工艺的系数不同,此处的系数相当于是构建了一个对称反相器
以两输入与非门和两输入或非门为例:
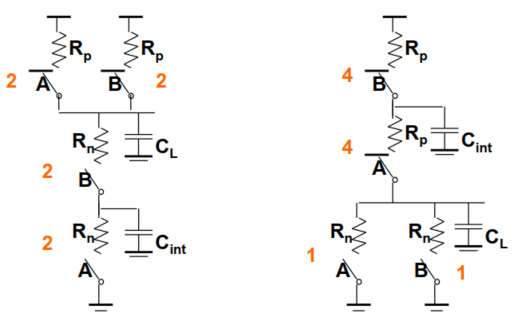
双输入与非门:
PUN:当只有一个管子导通的时候,取到最大电阻,$R_{PUN-max}=R_P$
PDN:当两个管子同时导通的时候,取到最大电阻,$R_{PDN-max}=2R_N$
即$R_P=2R_N$
假设$R_P=1$,则$W_P=2$;此时$R_N=1/2$,则$W_N=2·1=2$
结果如上图。
双输入或非门:
PUN:当两个管子同时导通的时候,取到最大电阻,$R_{PUN-max}=2R_P$
PDN:当只有一个管子导通的时候,取到最大电阻,$R_{PDN-max}=R_N$
即$2R_P=R_N$
假设$R_N=1$,则$W_N=1$;此时$R_P=1/2$,则$W_P=2·2=4$
结果如上图。
【重点】复合门的例子
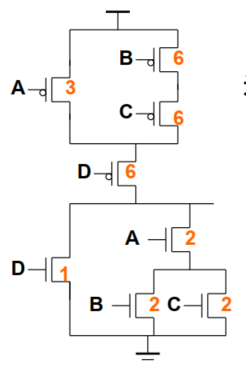
PUN:$B、C、D$管子 或 $A、D$管子导通时,取到最大电阻,$R_{PUN-max}=3R_{P-bcd}$或者$R_{PUN-max}=2R_{P-ad}$
PDN:$A、C$ 或 $A、B$导通 或 只有$D$管子导通时,取到最大电阻,$R_{PDN-max}=2R_{N-ac、ab}$或者$R_{PDN-max}=R_{N-d}$
即$2R_{P-bc}+R_{P-d}=R_{P-a}+R_{P-d}=R_{N-d}=R_{N-a}+R_{N-bc}$
假设$R_{N-d}=1$,则$W_{N-d}=1$;
若令$R_{N-a}=R_{N-bc}=R_{N-abc}$,即$2R_{N-abc}=R_{N-d}$,因此$R_{N-abc}=1/2$,$W_{N-abc}=2·1=2$
若令$R_{P-bc}=R_{P-d}=R_{P-bcd}$,即$3R_{P-bcd}=R_{N-d}$,因此$R_{P-bcd}=1/3$,$W_{P-bcd}=3·2=6$
又因为$2R_{P-bc}=R_{P-a}$,即$\frac{3}{2}R_{P-a}=R_{N-d}$,因此$R_{P-a}=2/3$,$W_{P-a}=\frac{3}{2}·2=3$
结果如上图。
或采用另外一种方法——更加方便快捷
PUN:$B、C、D$管子 或 $A、D$管子导通时,取到最大电阻。
取串联最多的,即$3R_{P-bcd}$为计算基准
PDN:$A、C$ 或 $A、B$导通 或 只有$D$管子导通时,取到最大电阻
取串联最多的,即$2R_{N-ac、ab}$为计算基准
对于PUN,因为最多是3个电阻串联——3(BCD),且为PMOS管——2,故$W_{P-bcd}=3·2=6$
根据$A$和2个电阻并联——2(BC),故$W_{P-a}=\frac{6}{2}=3$
对于PDN,因为最多是2个电阻串联——2(AB或AC),且为NMOS管——1,故$W_{N-abc}=2·1=2$
根据$D$和2个电阻并联——2(AB或AC),故$W_{N-d}=\frac{2}{2}=1$
3. Elmore延时模型
【用途】:用于大概估算具有众多电容、电阻电路的延时,适用于【RC树】
最基本的公式:
何为【RC树】?
电路仅有一个输入节点
电容均在节点和地之间
电路不包含任何电阻环路
两概念:路径电阻、共享路径电阻
- 路径电阻:输入节点到所求节点之间的唯一电阻通路上的电阻
- 共享路径电阻:输入节点到$i、A$两个节点之间共享的【路径电阻】上的电阻
如下图所示:
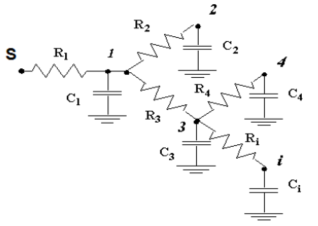
$i$节点的路径电阻$R_{ii}$:$R_1、R_3、R_i$;
1节点的路径电阻$R_{11}$:$R_1$
…
节点$i$、1的共享路径电阻$R_{i1}$:$R_1$
节点$i$、2的共享路径电阻$R_{i2}$:$R_1$
节点$i$、3的共享路径电阻$R_{i3}$:$R_1、R_3$
节点$i$、4的共享路径电阻$R_{i4}$:$R_1、R_3$
节点$i、i$的共享路径电阻$R_{ii}$:$R_1、R_3、R_i$;
…
可以看到,路径电阻可以认为是一种特殊的共享电阻。
于是有计算公式如下:
注意:计算延时的时候,电容$C_k$为RC树中的所有电容。也就是该RC树的延时和所有电容有关
以上文图中的RC树为例子
于是
4. 【Elmore延时】计算复合门延时——【多扇入】
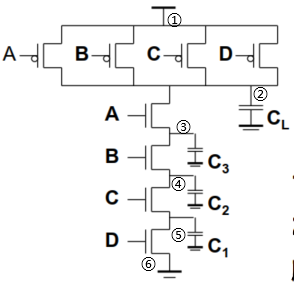
考虑延时的时候,常常考虑最坏的情况——所有的电容都充电或者所有电容都放电。
如果原本$ABCD=1110$,则此时所有电容均充电到$V_{DD}$
在零时刻,$ABCD=1111$,此时所有的电容进行放电。
此时$S=⑥,i=②、③、④、⑤$
即:
$⑤$节点$C_1$通过$R_{ND}$放电($1R$),
$④$节点$C_2$通过$R_{ND}+R_{NC}$放电($2R$),
$③$节点$C_3$通过$R_{ND}+R_{NC}+R_{NB}$放电($3R$),
$②$节点$C_L$通过$R_{ND}+R_{NC}+R_{NB}+R_{NA}$放电($4R$)
若NMOS管的电阻均相等,为$R_{eqn}$
于是,
分析【多扇入】:
- 晶体管串联导致电阻增大,传播延时随着扇入数的增大而增大
- 一个门的无负载本征延时最坏情况下,延时约为扇入数的二次函数
- 实际应用中,一般扇入数不超过4
5. 降低【多扇入】的电路的延时
调整管子尺寸
——逐级加大晶体管尺寸,即在Elmore分析中出现最多次的管子的电阻应该减小($W$增大)
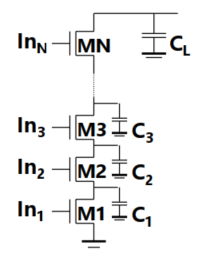
尺寸:$M_1>M_2>M_3>…>M_N$
缺点:画版图困难
重新安排输入
——关键路径上的晶体管应该靠近输出端。
关键信号:一个门的输出信号中,在所有输入中最后到达稳定的信号。
关键路径:决定一个结构最终速度的逻辑路径称为关键路径。
原理:越靠近输出端,信号需要经过的管子少,$RC$延时短。
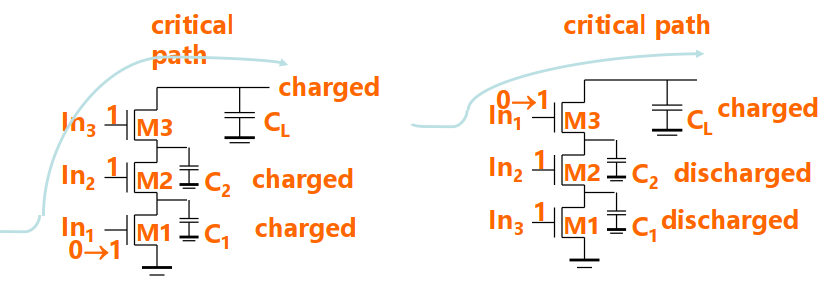
最坏情况,全部的电容放电——即下拉网络对地有通路。关键信号应为$0→1$,其他信号为$1$
如左图,关键输入信号远离输出端,则$In_1=0→1$时,$C_1、C_2、C_L$放电,延时最大。
如右图,关键输入信号靠近输出端,当$In_1$还等于$0$时,其他电容已经放电完毕。当$In_1=0→1$时,只有$C_L$放电,延时小。
重构逻辑结构
——多扇入逻辑电路拆解成若干个较低扇入的逻辑电路。
前面
Elmore延时模型已经知道,延时和扇入数接近平方关系增长。于是降低扇入数,可以降低电路的整体延时。
加入
buffer隔开大扇入和大扇出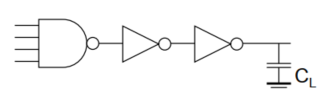
buffer的$C_G$比较小,一定程度上削弱了大扇入的延时;- 根据$C_L$的大小,按照$f=\sqrt[N]{F}$比例设置反相器的尺寸,可以降低大扇出带来的大延时。
6. 延时和【扇出】
公式:
一般,进行归一化后取$\gamma=1$,即有
呈现线性关系。
7. 总结
关于逻辑门的延时,给出如下的公式进行描述
$F_I$表示总的等效扇入,$F_O$表示总的等效扇出。
可见,延时与扇入成平方关系,同扇出成线性关系。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!