数字集成电路(12)运算单元(加法器)
本文最后更新于:2022年10月19日 下午
本人《数字集成电路设计》课程笔记,老师为王仁平。
本文主要讲述数据通路上的基本元件——加法器,包括一位全加器和多位全加器。
第十一章 设计运算功能块
1. 总论
在时序电路中,时序电路=组合电路+存储电路
在(9)~(11)中,已经详细介绍了存储电路(寄存器)
在本文中,将介绍组合电路中比较重要的数据通路上的电路,可以认为是在时序电路中提到的$logic$,即用于逻辑运算和算数运算。
在数集中,常用的数据通路组合电路有
- 加法器
- 乘法器
- 移位器
我们的目的,是追求以下几个方面的优化
- 性能
- 面积
- 功耗
如何优化:
- 逻辑层次优化:利用状态机、真值表等,优化布尔方程得到一个速度更快、面积更小的电路
- 电路层次优化:改变管子的尺寸;改变电路的拓扑连接(互补CMOS、动态CMOS等)
2. 加法器
加法器在数据通路电路中的地位类似于反相器在与或等简单逻辑电路的位置
数据通路的电路的基础是加法器
乘法器也是加法器扩展而来的
加法器是限制数据通路运算速度的元件。
1. 一位全加器($FA$)
1. 传统表达方式
定义:根据输入的二值数据、进位信号,计算得到结果和进位。
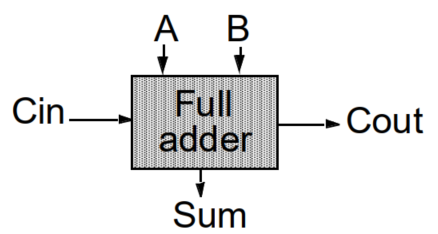
其中,
$A、B$:输入的数据,或为0、或为1
$Cin/\ C_{i}$:输入的前级的进位信号,或0或1
$Sum/\ S$:计算得到的结果
$Cout/\ C_o$:计算得到的进位信号
其逻辑关系为
【注】:
$\bigoplus$:异或,常见结构有:
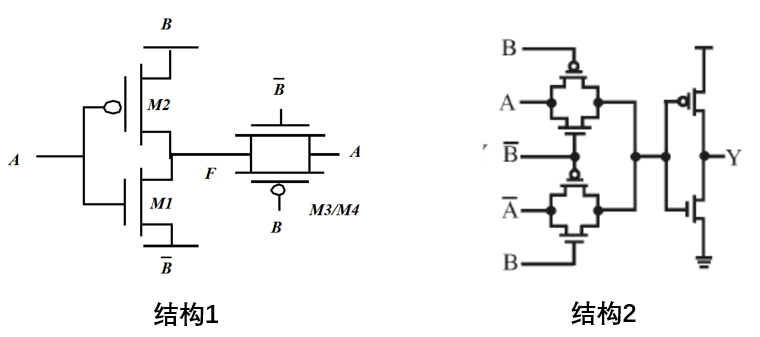
$\bigodot$:同或,结构如下(即“异或门结构2”的“非”):
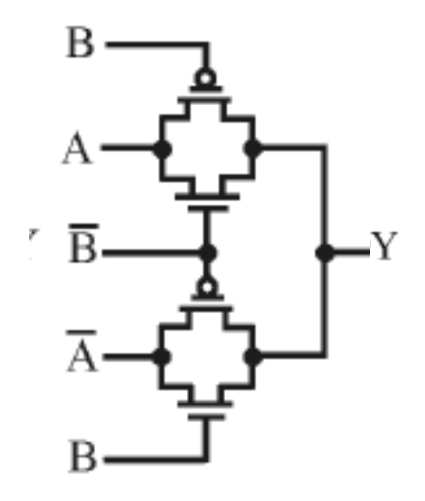
2. $P、G、D$函数表达
真值表如下:
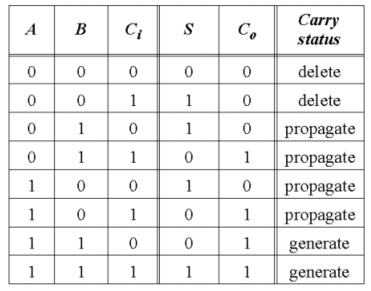
$P、G、D$的表达式如下(根据真值表可得):
现对$P、G、D$进行解释:
$P$:只要$P=1$,则只要$C_i=1$,即前级有进位,则本级进位输出$C_o$输出等于1。故称,$P$为进位传播。
$G$:只要$G=1$,则本级进位输出$C_o=1$,且与$C_i$无关,故称$G$为进位产生。
$D$:只要$D=1$,则本级进位输出$C_o=0$,且与$C_i$无关,故称$D$为进位取消
注意:三者为互斥
将$f(A,B,C_i)$改写为$f(P,G(或D))$,即有
小贴士:
- $G$和$D$在表征进位上功能类似,其值直接表征了$C_o$的输出值,与$C_i$的输入无关。故而常常把二者合一(如上式,仅用$P、G$作为自变量)。
- $P、G(或D)$的值仅仅与$A、B$值有关,而与$C_i$无关
- 用这三个中间变量表征$S、C_o$十分有用
3. 逐位(行波)加法器
所谓逐位(行波)加法器,指的是将$N$个一位全加器($FA$)串联在一起构成加法器。如下图
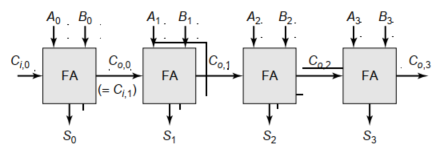
此处主要讨论其性能(延时)。
根据电路图,可知,设计行波加法器,提高优化进位运算$t_{carry}$比优化和运算$t_{sum}$重要得多。
原因:由图可知,输入各级$FA$的信号中,$A、B$在理想状态下,在零时刻即输入到各级$FA$的输入端;而$C_i$需要等待上一级运算之后,才能到达本级$FA$的输入端。故,关键信号是$C_i$(概念见(4).5.3),只有提高$t_{carry}$,才能从根本上优化行波加法器的运算速度。
最坏情况,$t_d=O(N)$
最坏情况下,延时正比于全加器串联级数$N$
2. 【结构】设计全加器FA
1. 互补静态CMOS结构FA
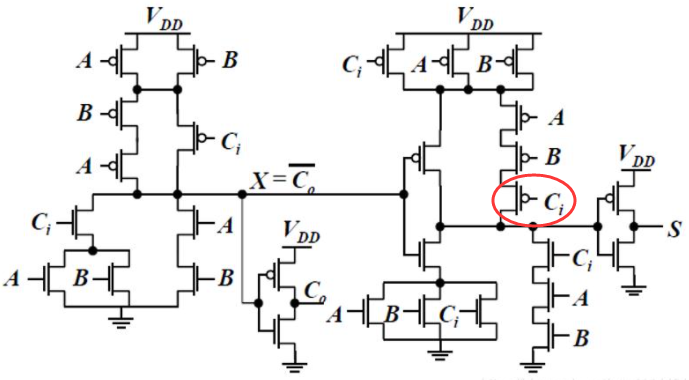
根据电路图可知,该电路对一些逻辑进行了变化
| 传统 | 该电路 | 备注 |
|---|---|---|
| $C_o=AB+BC_i+AC_i$ | $C_o=AB+BC_i+AC_i$ | 未改变 |
| $S=A\bigoplus B \bigoplus C_i$ | $S=ABC_i+\overline{C_o}(A+B+C_i)$ | 改变 |
优点:
- 可知,$S$在计算的时候,复用了$C_o$的逻辑,使得管子数量有所减小,一共使用了28个管子
- 【小技巧】在(4).3.5中已经提到,关键信号应该靠近输出端。如图中红圈,$C_i$
缺点:
——(主要考虑对于$C_o$的影响)——工作速度较慢:
- 虽然管子数量有所减少,但是28个管子依旧消耗了较大的面积
- 作为关键信号$C_o$,其产生电路中堆叠了太多的PMOS管(?为啥提到PMOS管)
- $C_o$的本征负载电容很大,根据$t_p=C_L·R_{eq}$可知,产生$C_o$的延迟较大
2. 镜像加法器
该加法器是根据互补静态CMOS结构FA改进得到的,镜像加法器的下拉网络和互补CMOS结构FA完全相同。
电路图如图所示,
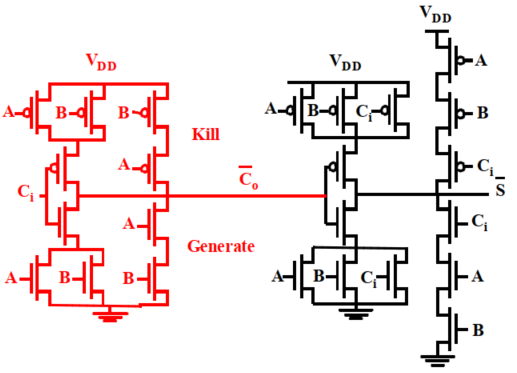
| 项目 | 公式 |
|---|---|
| 进位输出:$\overline{C_o}$ | $\overline{C_o}=\overline{AB+(A+B)C_i}$ |
| 求和输出:$\overline{S}$ | $\overline{S}=\overline{ABC_i+\overline{C_o}(A+B+C_i)}$ |
注意点:
- 24个管子
NMOS管(下拉网络)和PMOS管(上拉网络)完全对称,利用的是 求和 和 进位 的”自对偶性”
同互补CMOS加法器,关键信号$C_i$应该靠近输出端。
进位输出电路需要考虑管子尺寸匹配问题,提高进位运算速度。
求和输出电路不需要考了管子尺寸,可以全部使用最小尺寸。
- ⭐需要掌握镜像加法器的棍棒图
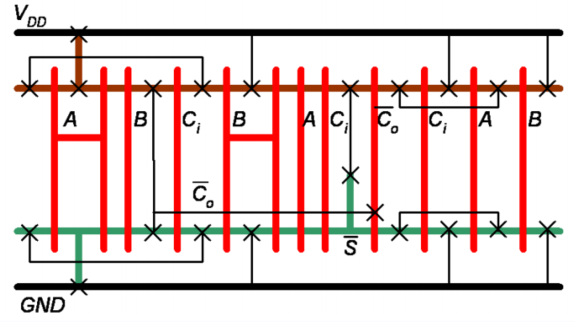
3. 传输门型加法器——传统型
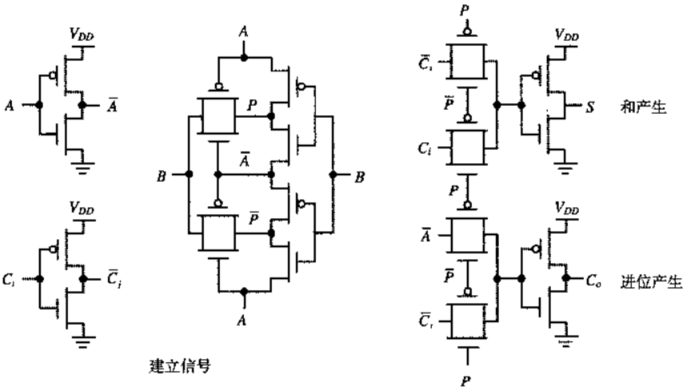
注意点:
24个管子
使用模块:多路开关+反相器
进位产生和求和输出的延时几乎相同
真值表
| 结果\建立信号 | $P=0$ | $P=1$ |
| :—————-: | :—-: | :———————: |
| $S$ | $C_i$ | $\overline{C_i}$ |
| $C_o$ | $A$ | $C_i$ |
4. 传输门型加法器——曼切斯特FA
1. 静态电路
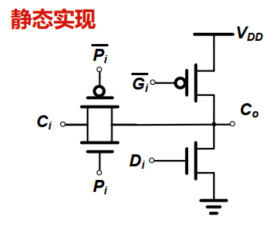
分析:
第一部分:传输门
该传输门的表达式很容易写,为:$C_iP_i$
因为$P、G、D$互斥,当$P_i=1$时,$D_i=0$且$G_i=0(\overline{G_i}=1)$,第二部分上下拉网络均截止,输出取决于$C_i$
第二部门:上下拉网络
当$P_i=0$时,根据互斥原理,存在以下两种情况:
当$D_i=1$时,表示进位为0,故输出需要下拉到地,即下拉网络导通,故下拉网络栅极输入为$D_i$
当$G_i=1$时,表示进位为1,故输出需要上拉到$VCC$,即上拉网络导通,又因为上拉网络需要栅极输入为0时才能实现上拉功能,故上拉网络的栅极输入为$\overline{G_i}$
2. 动态电路
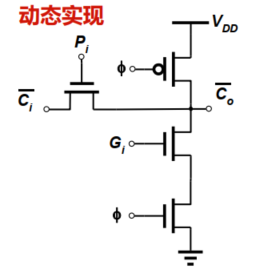
- 动态电路简单
- 动态电路单向工作,传输门使用NMOS管实现
- 该电路不需要$D$
3. 曼切斯特进位链加法器
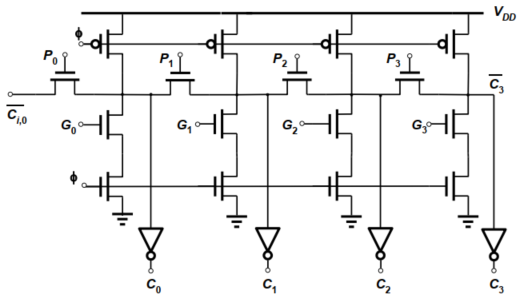
最坏情况:
$P_0P_1P_2P_3=1111$,则$G_0G_1G_2G_3=0000$,当$\overline{C_{i,0}}=0$时,电路通过$P_0$、$P_1P_0$、$P_2P_1P_0$、$P_3P_2P_1P_0$放电,可知最坏情况下,$t_p=O(N^2)$(1+2+3+4…)
4. 【会画会认】两位曼切斯特进位链棍棒图
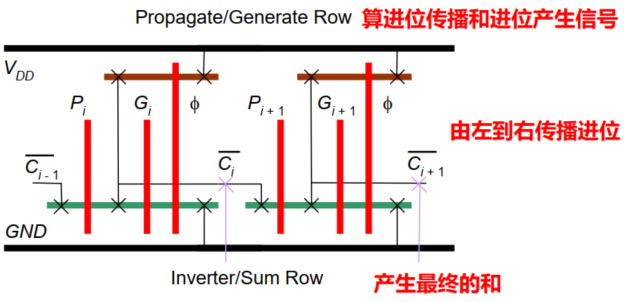
特点:
- 动态逻辑上下管子数差很多,上少下多。
3. 【逻辑】设计全加器FA
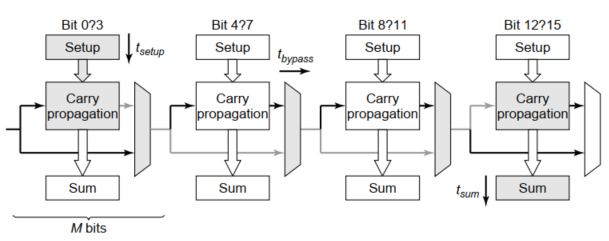
1. 旁路进位加法器
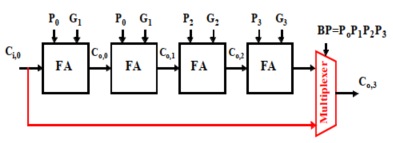
当$BP=P_0P_1P_2P_3=1$时,即最坏情况下,可以直接得到$C_{o,3}=C_{i,0}$;
只要有一个$P=0$,则只能按照正常路径计算进位。
特点:逐位加法器进行最坏情况优化缺点:
- 对速度提升不多,一般用得很少
- 主要考虑了最坏情况单种情况,对速度提升不大
- 增加了旁路,使得电路不够规则,画版图不方便
优点:
- 速度提升虽然不多,但是面积增加也不多。
- 速度的提升在高位进位时显现优势。
延时(了解):
$t_{adder}=t_{setup}+Mt_{carry}+(\frac{N}{M}-1)t_{bypass}+(M-1)t_{carry}+t_{sum}$
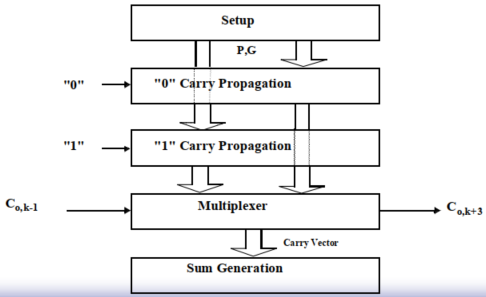
2. 线性进位选择加法器
缺点:
- 以面积换取速度,使得整个放大器的面积大大增加。
优点:
- 速度提升了
延时:
$t_{adder}=t_{setup}+Mt_{carry}+(\frac{N}{M})t_{mux}+t_{sum}$
实际上,由于第一级只需要计算出$P、G$就可以直接根据$C_{i,0}$得到$C_{o,1}$,故第一级不需要选择器。
因此延时公式修正为:$t_{adder}=t_{setup}+Mt_{carry}+(\frac{N}{M}-1)t_{mux}+t_{sum}$
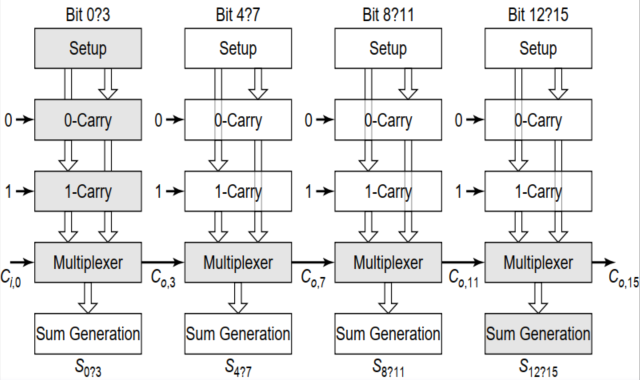
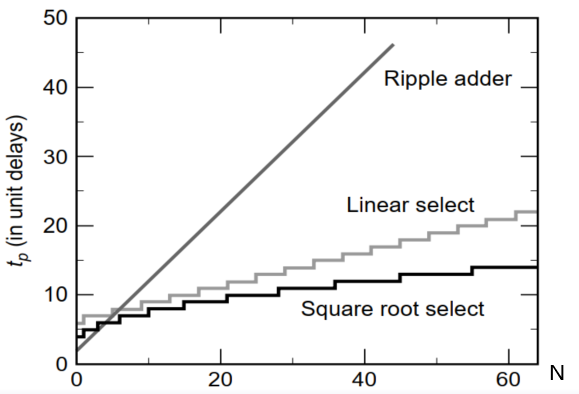
3. 平方根进位加法器
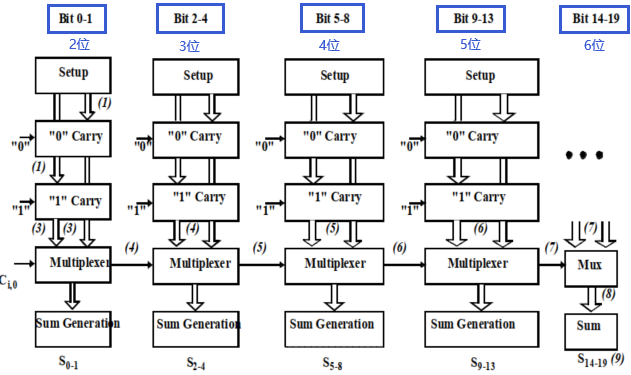
优点:运算速度最快
延时:
$t_{adder}=t_{setup}+Mt_{carry}+(\sqrt{2N})t_{mux}+t_{sum}$
4. 小结
| 加法器 | 传统FA:逐位加法器 | 旁路进位加法器 | 线性进位加法器 | 平方根进位加法器 |
|---|---|---|---|---|
| 速度 | ※ | ※※ | ※※※ | ※※※※ |
| 优点 | 规规矩矩 | 考虑了最坏情况 | 实现计算好两种$C_i$的情况,【等待真实$C_i$信号】到来然后进行选择 | 【一边】计算好两种$C_i$的情况,【一边】根据$C_i$进行选择 |
| 备注 | 每个单元都是M位的运算 | 单元的运算位数逐级递增 |
5. 超前进位加法器
见下文
4. 【重要】超前进位加法器
1. 原理
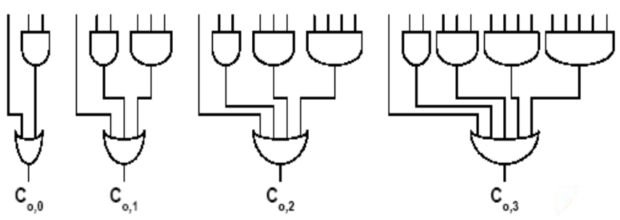
根据$C_{o,k}=G_k+C_{o,k-1}P_k$可知只要将$C_{o,k-1}$利用递归拆开,就可以让$C_{o,k}$摆脱$C_{o,k-1}$的束缚,使得
只要知道了各级的$G、P$和最初的$C_{i,0}$即可计算出$C_{o,k}$。
容易知道,只要经过简单的逻辑运算:$G=AB$、$P=A\bigoplus B$即可得到数据,而$C_{i,0}$是输入信号之一。
缺点:随着计算位数的增多,整个加法器的扇入非常大。
一些电路图:
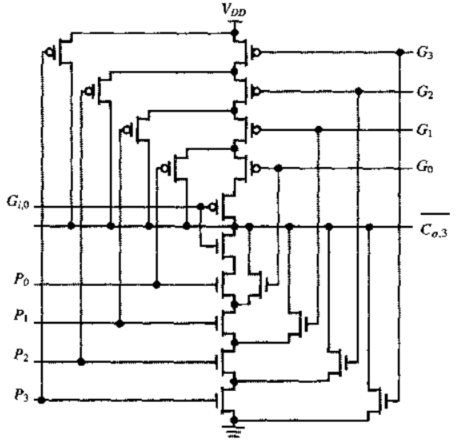
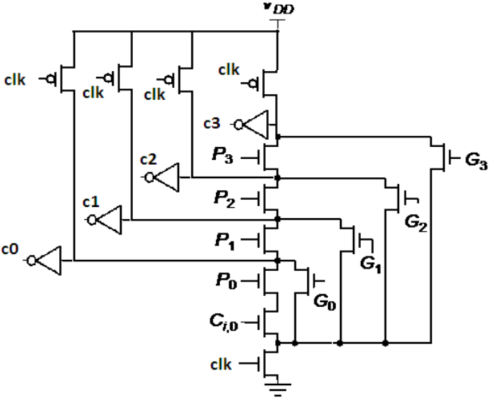
2. 块运算
令:
$G_{a:b}$和$P_{a:b}$分别表示从第$a$位到第$b$位的进位产生和进位传播信号,称为块进位产生和块进位传播
$eg:$
$G_{2:0}=G_2+P_2G_1+P_2P_1G_0$
$G_{3:1}=G_3+P_3G_2+P_3P_2G_1$
$P_{3:0}=P_3P_2P_1P_1$
$P_{3:1}=P_3P_2P_1$
经过推导,有
即:只要算出块进位产生和块进位传播,就可以轻松算出任何一位的进位输出
其中,
$C_{o,k}$:第$k$级的进位输出
$G_{k:0}$:第$k$级到第$0$级的块进位产生
$ P_{k:0}$:第$k$级到第$0$级的块进位传播
$C_{i,0}$:第0级的进位输入,即加法器系统的进位输入
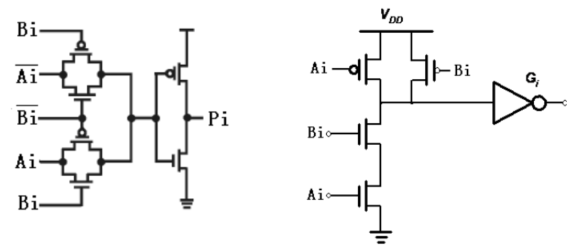
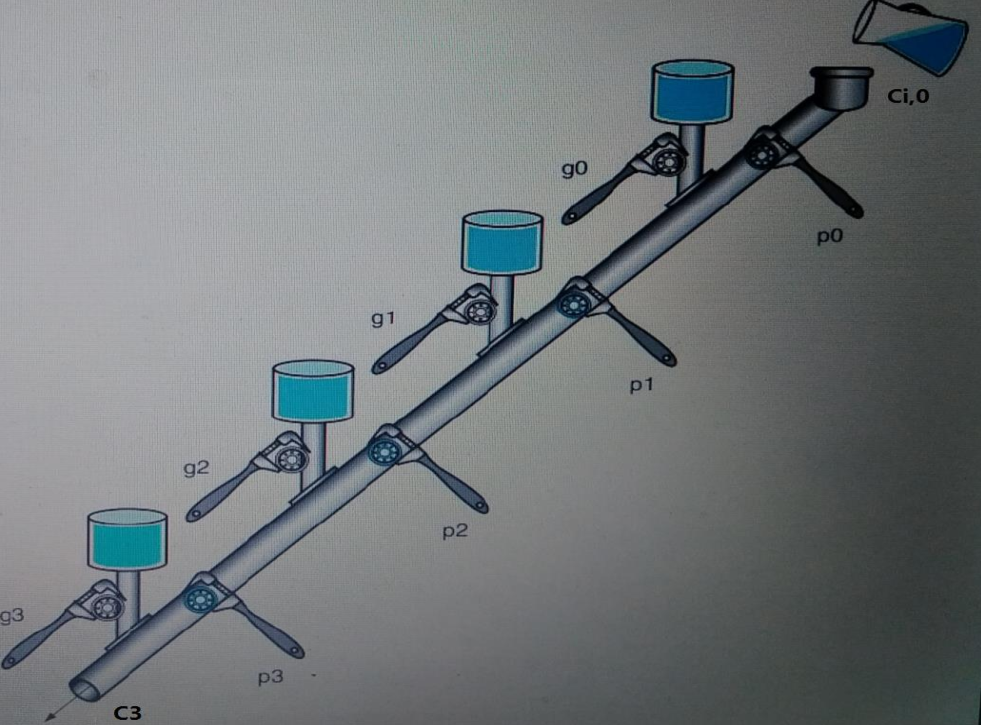
根据上图,可以很形象理解,并且得到以下式子
3. 点操作
步骤如下:
判断计算位数,分别计算出各个$G_k,P_k$
其中:$G_k=A_kB_k$、$P_k=A_k\bigoplus B_k$
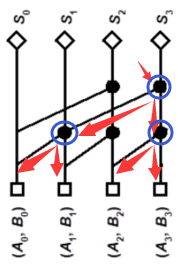
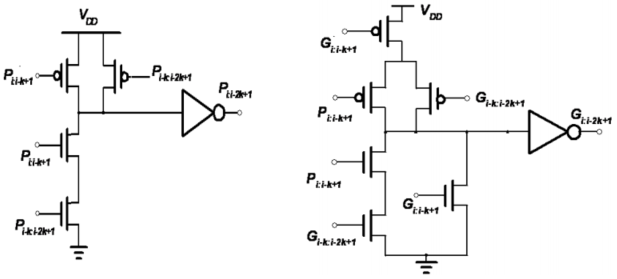
上图分别是使用静态逻辑实现的进位传播、进位产生
根据你要求的$C_{o,k}$列出表达式
即:
根据2得到的$G_{k:0}$、$P_{k:0}$列出点操作表达式,下面以4位加法器为例子
列式子
$(G_{3:0},P_{3:0})=(G_3,P_3)·(G_2,P_2)·(G_1,P_1)·(G_0,P_0)\$
$=[(G_3,P_3)·(G_2,P_2)]·[(G_1,P_1)·(G_0,P_0)]$
$=(G_{3:2},P_{3:2})·(G_{1:0},P_{1:0})$
$=(G_{3:2}+P_{3:2}G_{1:0},P_{3:2}P_{1:0})$
此时已将多位加法器转换为2位加法器
画出树结构图
最上面一个点,表示$(G_{3:0},P_{3:0})$
中间两个点分别为$(G_{3:2},P_{3:2})$和$(G_{1:0},P_{1:0})$
最下面四个方块点分别为$(G_3,P_3)、(G_2,P_2)、(G_1,P_1)、(G_0,P_0)$
计算各个节点:
根据上文块运算已知,以其中一个节点$(G_{1:0},P_{1:0})$为例
$G_{1:0}=G_1+P_1G_0$
$P_{1:0}=P_1P_0$
再如节点$(G_{3:0},P_{3:0})$为例
$G_{3:0}=G_{3:2}+P_{3:2}G_{1:0}$
$P_{3:0}=P_{3:2}P_{1:0}$
即2位的块运算,只需要简单的一个或-与门和与门就可以完成运算。
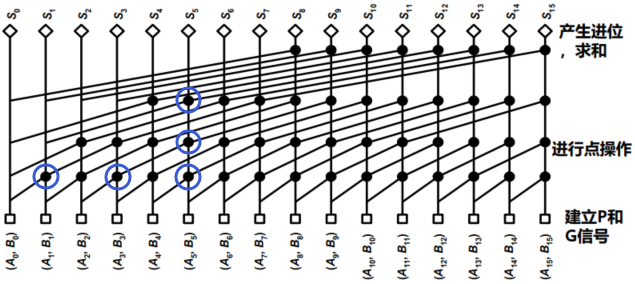
4. Kogge-Stone 16位超前进位加法器
运算速度快。
在位置$2^i-1$上的进位,只需要$i$次操作就可以计算出来。
面积、功耗较大
关键路径上的扇出基本是一个常数
互连结构,实现容易
例子:计算$C_5$
- $C_5=G_{5:0}+P_{5:0}C_{i,0}$
- 注意:需要严格按照图中的连线来
小贴士:
- 需要严格按照图中连线,否则将判定为错误。
- 有几层节点,就需要写几行
5. Brent-Kung 16位超前进位加法器
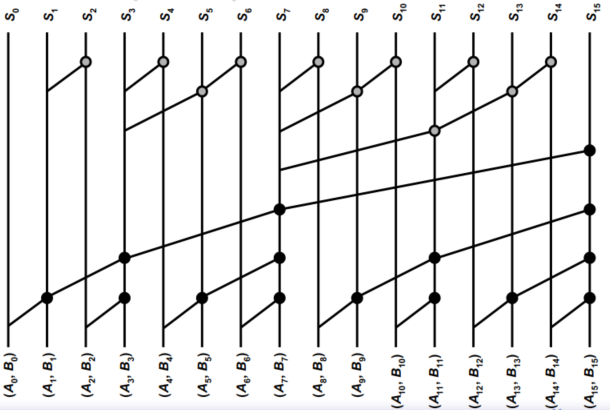
分为正向树和反向树。如图,黑点为正向树,灰点为反向树。
正向树只计算$2^N-1$的点,如图中0、3、7、15位;反向树利用正向树计算出来的节点,补全其他位
布线少,但是布线不规则
每个门的扇出不同,优化困难
不同于K-S加法器,在位置$2^{i-1}$~$2^i-1$上的进位,只需要$i$次操作就可以计算出来。
B-K 16位加法器中,最长路径的$C_{14}$需要计算6个节点
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!